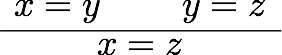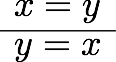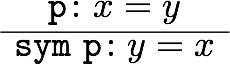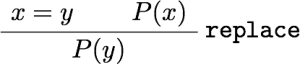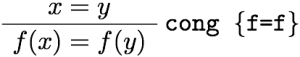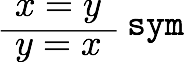11月22日から24日にかけて行われた東京大学駒場キャンパスでの第65回駒場祭で、数学科有志による「ますらぼ」企画(@UTmathlabo)に参加していました。「ますらぼ」では、数学科生・院生による発表、我々で作った冊子の配布、それから数学に関する展示が行われていました。
私は、かねてから作っていた複素関数を視覚化するWebアプリケーション “Conformality” に関する記事を書いたり、展示をしたりしていました。
冊子には、いくつかの複素関数の例・解説と、Webアプリの舞台裏に関する記事を書きました。一方、展示では、いくつかの複素関数の例・解説をポスター(というほどの紙の大きさでもない)で貼ったのと、パソコンとタブレットを用意して実際にWebアプリを動かしながら解説するのをやりました。
来場者に解説するとき、聞き手のレベルに合わせて話して、分かってもらうのは楽しかったです。実際どのぐらい理解してもらえたかは不明ですが…。あと、ふだんあまり喋らないので声が枯れました。
具体的に、レベルに応じてどんな内容を話したかというと、
小学生(!)
- そもそも0や負の数はまだ習っていないので、まずはそこから。
- 複素数の足し算が平行移動になることを説明できれば十分すぎるだろう。
中学生
- 実数はOK。「数直線の数」みたいな感じ。
- 複素数を紹介。いずれ高校で習うよ、ということで。
- 複素数のかけ算ぐらいまでは解説しただろうか?
- 「関数」としては \(y=ax^2\) ぐらいがいいとこだったかな?と思ったが、中学校では「関数」として「一次関数」というのが出てくるのを失念していた。
高校生
- 現行の学習指導要領では数学IIIで複素数平面を扱う。複素数自体は、もっと前の2次方程式関連のところで出てくるはず。(高校では「複素数平面」というようだが、数学が専門の人は普通は「複素平面」と言う。私のような面倒くさがりな人には1文字少ないのはでかい)
- 学年としては、3年生は複素数平面知っているはず。2年生の11月では複素数平面をやっている学校があるかないか、という感じ。聞いてみたところ「明日(火曜日)から複素数平面の単元に入る」という人もいた。
- 事前に書店などに出向いて数学IIIの参考書を立ち読みしたところ、高校で扱うのは(今回関係ありそうなのは)複素数のかけ算の図形的な意味やド・モアブルの定理がせいぜいだということが分かった。
- 今は高校で行列を教えないので、一次分数変換と行列の関係を教えにくかった。
- 高校では実数の指数関数や三角関数を習う。
大学生
- 複素数や複素平面はまあ知っている(1、2年生や、文系の3、4年生も含めて)。
- 理系の3、4年生には一次分数変換の円円対応や正則関数の等角性まで知っている人もいて話が早かった。
という感じでした。
教える関数としては、当初は一次分数変換が一番単純かなあと思いましたが、高校生を視野に入れるなら複素数のかけ算(拡大縮小と回転)からやった方が学習の役にも立つだろうと思って、冊子やポスターでは最初に複素数のかけ算の例を載せました。しかし、実際に人に教えるときはもっと初歩的な、複素数の足し算の幾何学的意味(平行移動)から始めたので、他人への解説の仕方というのは自分だけで考えてもわからないものだということを認識しました。
解説内容はそのうちこのブログかどこかに載せたいと思います(時間があれば)。
余談として、「ますらぼ」の教室では学内無線LANが使えないので、Webアプリケーションを動かすには工夫が必要でした。持ち込んだ機器は
- MacBook
- 解説の際の主力。
- ペアレンタルコントロールを設定したアカウントでWebブラウザを動かした。
- セキュリティースロットにワイヤーをつけて盗まれないようにした。6年半前にこのMacBookを買ってから初めてセキュリティースロットが活躍した。
- Nexus 7
- 画面が小さいので微妙に使いづらかった。
- 制限アカウントを作って使ってもらった。
- タブレット本体にはセキュリティースロットがないので、サンワサプライの7インチタブレット向け盗難防止用具
を買ってそれにワイヤーをつけた。
- AirMac Express
- Nexus 7とMacBookを同一ネットワークにつなげた。
で、MacでWebサーバーを動かしてWebアプリケーションを動かす感じにしました。URLは本来の “https://miz-ar.info/webapp/conformality/” で動いているように見せたかったので、MacBookとNexus 7で d-poppo.nazo.cc がMacBookのIPアドレスに解決されるようにしました。
ドメイン名に対して好き勝手なIPアドレスを割り当てるためには /etc/hosts をいじるのが手軽な方法だと思います。しかし、Androidの場合は /etc/hosts をいじるにはroot権限を取る必要があり、調べてみたところ思いの外危なそう&面倒くさそうだなあと思ったので、代わりに手元でDNSサーバーを動かすことにしました。MacBookにはDNSサーバーのソフトウエア(BIND9)が搭載されていた(最新のOSXにはないらしい)のですが、駒場祭直前にBIND9の使い方なんて覚えられない…。と思っていたらWebminとかいう便利なツールがあることを知ったので軟弱者の私はそれでBIND9を設定しました。めでたしめでたし。