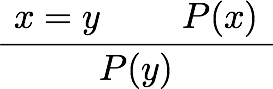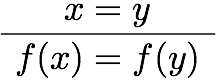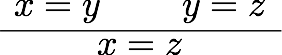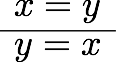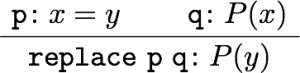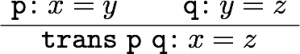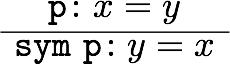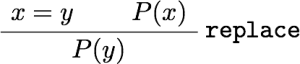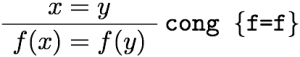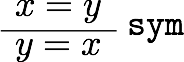Idrisで遊んでみた (1)

前回はIdrisで2つの自然数を比較し、結果とその証明を返す関数 compareNats を作った。今回は、それに追加していくつかの関数を実装してみる。

まず、二つの自然数 \(x\) と \(y\) の差、\(x-y\) を計算する関数 difference を作る。\(y\le x\) の場合は良いが、\(x\lt y\) の場合はどうするか考えどころである。0を返すようにしてもよいが、ここは「\(y\le x\) であることの証拠を要求する」ことにして、\(x\lt y\) の場合は考える必要がない、という仕様にする。型を書けば
[sourcecode lang=”plain”]
difference : (x:Nat) -> (y:Nat) -> LTE y x -> Nat
[/sourcecode]
となる。前回書いたように、LTE y x は命題 \(y\le x\) に対応する型である。

実装には、例によって引数によるパターンマッチをする。

\(y=0\) の場合
- \(x\) を返す。第三引数は lteZero である。
- コードで書けば difference x 0 lteZero = x となる。
\(x=Sx’, \>y=Sy’\) の場合
- 第3引数は lteSucc p の形をしている。
- difference x' y' p によって \(x’-y’\) を計算できる。\(x-y=x’-y’\) なので、それをそのまま返せば良い。
- コードで書けば difference (S x') (S y') (lteSucc p) = difference x' y' p となる。

まとめると
[sourcecode lang=”plain”]
difference : (x:Nat) -> (y:Nat) -> LTE y x -> Nat
difference x 0 lteZero = x
difference (S x’) (S y’) (lteSucc p) = difference x’ y’ p
[/sourcecode]
となる。

さて、よく考えてみると、第1引数 x と第2引数 y の情報は第3引数の型を見れば自動的に得られる。したがって、第1引数と第2引数は省略できるのではないか？

Idrisにはimplicit argumentsという機能があるので、この場合実際に x と y を省略できる。Implicit argumentsを使うと、difference は次のように書ける:
[sourcecode lang=”plain”]
difference : {x:Nat} -> {y:Nat} -> LTE y x -> Nat
difference {x} lteZero = x
difference (lteSucc p) = difference p
[/sourcecode]

この difference という関数は、\(y \le x\) を満たす任意の自然数 \(x\), \(y\) および \(y \le x\) の「証拠」p : LTE y x に対して、\[x = y + \mathtt{difference}\>p\]という関係を満たす。この関係式を「証明」するにはどうすればよいだろうか？

その前に、述語論理における等号の公理と、それがIdrisではどうなっているか見ておこう。自然演繹チックに書けば、述語論理の等号の公理と関連する推論規則は