$\require{AMScd}\def\Real{\mathbf{R}}\def\Complex{\mathbf{C}}\newcommand{\abs}[1]{\left\lvert #1\right\rvert}$次の形をした複素関数 $f$ を一次分数変換という: $$f(z)=\frac{az+b}{cz+d},\quad \text{ただし \(ad-bc\ne0\).}$$ 分母が0になるとき（$z=-d/c$ のとき）は $f(z)$ の値は複素数としては定まらない、のだが、値が複素数であることにこだわらなければここは $\infty$ としておくのが都合がいい。逆に、$z=\infty$ のときは、（$z\to\infty$ の極限を考えれば分かるように）$f(z)$ の値は $a/c$ として定義できそうである。何がいいたいかと言うと、一次分数変換は、複素平面の関数というよりは、複素平面に「無限遠点」を加えたもの $\Complex\cup\{\infty\}$ の関数をみるのが自然である。

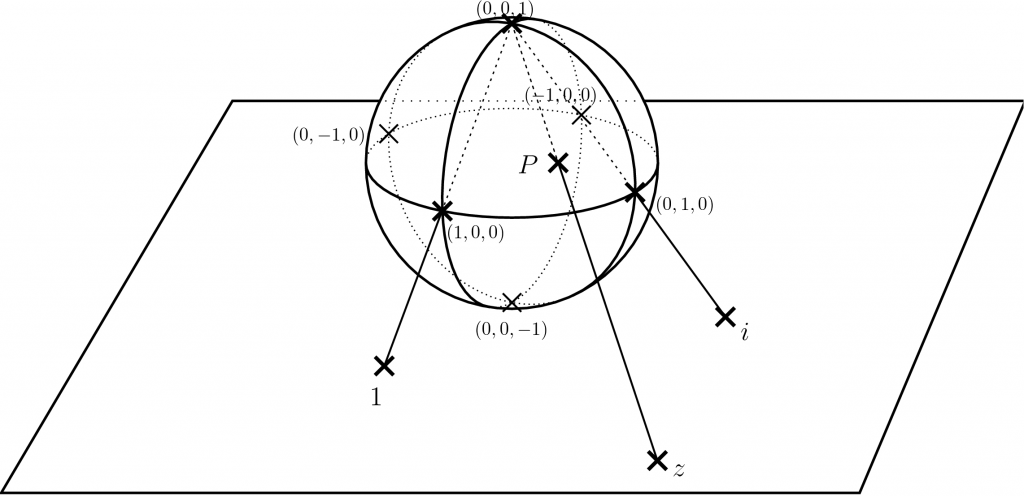
複素平面に無限遠点を加えたもの $\Complex\cup\{\infty\}$ は、球面と同一視できる（こうやって同一視したものをリーマン球面という）。球面上の点 $P$ に複素平面の点 $z$ をどう対応させるかというと、球の北極 $(0,0,1)$ から $P$ に直線を引いて、その直線が複素平面と交わる点 $z$ を対応させる。逆に、複素平面の点 $z$ に対しては、$z$ と北極 $(0,0,1)$ を結ぶ直線を引いて、それが球面と交わる（北極じゃない方の）点 $P$ を対応させる。北極に対応する点は複素平面上にはないので、北極には無限遠点 $\infty$ を対応させる。この対応を立体射影(stereographic projection)という。

続きを読む →

$\def\Real{\mathbf{R}}\def\Complex{\mathbf{C}}\newcommand{\ip}[2]{\left\langle #1,#2\right\rangle}\newcommand{\vect}[1]{#1}\def\Ker{\operatorname{Ker}}\newcommand{\restrict}[2]{\left.#1\right\rvert_{#2}}\newcommand{\transpose}[1]{{#1}^T}\newcommand{\abs}[1]{\left\lvert #1\right\rvert}$特殊直交群 $SO(n)$ が（弧状）連結であることを示すのはこの記事に書いたやり方がおそらく正攻法なのだろうが、次元が低い時はもっと短い議論でできるんじゃないかなあと思った。

続きを読む →

$\def\Real{\mathbf{R}}\def\Complex{\mathbf{C}}\newcommand{\ip}[2]{\left\langle #1,#2\right\rangle}\newcommand{\vect}[1]{#1}\def\Ker{\operatorname{Ker}}\newcommand{\restrict}[2]{\left.#1\right\rvert_{#2}}\newcommand{\transpose}[1]{{#1}^T}$特殊ユニタリ群 $SU(n)$ や特殊直交群 $SO(n)$ が（弧状）連結であることは当たり前のようにバンバン使うけど自分でそらで証明できるか怪しいなあと思ったので、証明をつけてみることにした。
続きを読む →