次の形をした複素関数 \(f\) を一次分数変換という:\[
f(z)=\frac{az+b}{cz+d},\quad \text{ただし \(ad-bc\ne0\).}
\]分母が0になるとき(\(z=-d/c\) のとき)は \(f(z)\) の値は複素数としては定まらない、のだが、値が複素数であることにこだわらなければここは \(\infty\) としておくのが都合がいい。逆に、\(z=\infty\) のときは、(\(z\to\infty\) の極限を考えれば分かるように)\(f(z)\) の値は \(a/c\) として定義できそうである。何がいいたいかと言うと、一次分数変換は、複素平面の関数というよりは、複素平面に「無限遠点」を加えたもの \(\Complex\cup\{\infty\}\) の関数をみるのが自然である。
複素平面に無限遠点を加えたもの \(\Complex\cup\{\infty\}\) は、球面と同一視できる(こうやって同一視したものをリーマン球面という)。球面上の点 \(P\) に複素平面の点 \(z\) をどう対応させるかというと、球の北極 \((0,0,1)\) から \(P\) に直線を引いて、その直線が複素平面と交わる点 \(z\) を対応させる。逆に、複素平面の点 \(z\) に対しては、\(z\) と北極 \((0,0,1)\) を結ぶ直線を引いて、それが球面と交わる(北極じゃない方の)点 \(P\) を対応させる。北極に対応する点は複素平面上にはないので、北極には無限遠点 \(\infty\) を対応させる。この対応を立体射影(stereographic projection)という。
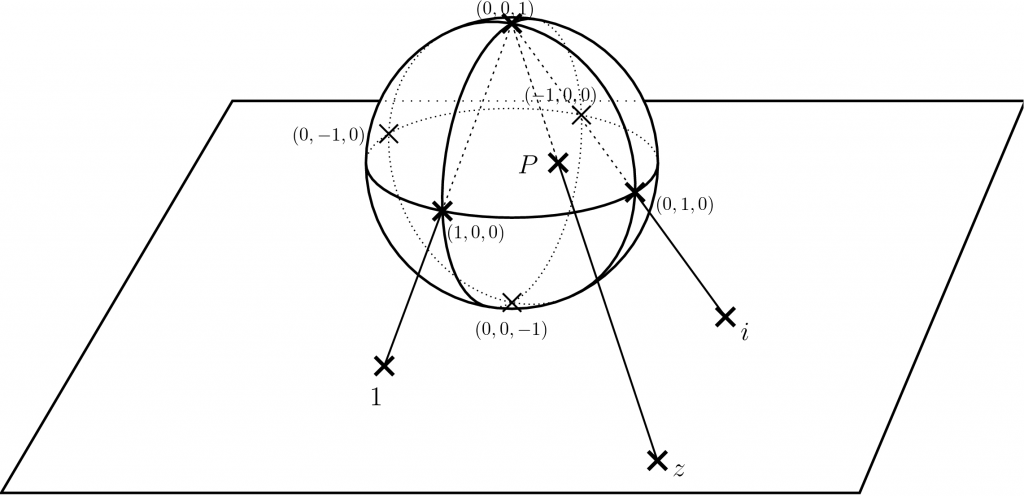
文章でごちゃごちゃと書いたが、数式で書くと以下のようになる。(\(S^2\) とは球面を表す記号である。ここでは3次元ユークリッド空間 \(\Real^3\) に埋め込んで考えている)\[
\begin{array}{rccc}
\varphi\colon&\Complex\cup\{\infty\}&\longrightarrow&S^2 \\
&z&\longmapsto&\frac{1}{\abs{z}^2+1}(2\operatorname{Re}z,2\operatorname{Im}z,\abs{z}^2-1) \\
&\infty&\longmapsto&(0,0,1)
\end{array}
\]逆向きの対応は\[
\begin{array}{rccc}
\varphi^{-1}\colon&S^2&\longrightarrow&\Complex\cup\{\infty\} \\
&(X,Y,Z)&\longmapsto&\frac{X+iY}{1-Z}&(Z\ne1 \text{の場合}) \\
&(0,0,1)&\longmapsto&\infty
\end{array}
\]で与えられる。(この対応を以後 \(\varphi\) で表す)
一次分数変換は、リーマン球面に対する行列の作用だと見なせる。行列 \(A\) の成分が\[
A=\begin{pmatrix}a&b\\c&d\end{pmatrix}\in GL(2,\Complex)
\](ここで \(GL(2,\Complex)\) というのは、行列式 \(ad-bc\) が0でない2次の複素正方行列全体のことであり、一般線型群(general linear group)という)のとき、 \(A\) の \(z\in\Complex\cup\{\infty\}\) に対する作用(action)を\[
A\cdot z=\frac{az+b}{cz+d}
\]により定める。「作用」というのは、次の2つの性質が成り立つことを言う。(\(I\) は単位行列である)\begin{align*}
I\cdot z&=z \\
(AB)\cdot z&=A\cdot(B\cdot z)
\end{align*}つまり、単位行列(群の単位元)を作用させても何も変わらないことと、先に行列の積を計算してから一次分数変換として作用させるのと2回に分けて一次分数変換として作用させることが一致していることである。
さて本題。
一次分数変換はリーマン球面からリーマン球面への変換だが、ある種の一次分数変換はリーマン球面に回転として作用する。例えば、絶対値1の複素数 \(e^{i\theta}\) をかける一次分数変換\[
\begin{pmatrix}e^{i\theta}&0\\0&1\end{pmatrix}\cdot z=e^{i\theta}z
\]を、リーマン球面で見るとZ軸を回転軸とする回転になっている。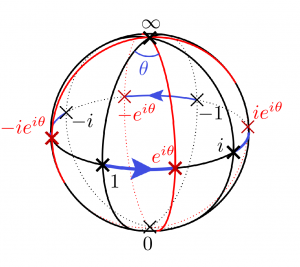
この回転を \(SO(3)\) の行列として \(R_Z(\theta)\) と書くことにすれば\[
R_Z(\theta)=\begin{pmatrix}
\cos\theta&-\sin\theta&0\\
\sin\theta&\cos\theta&0\\
0&0&1
\end{pmatrix}
\]となる。一次分数変換 \(e^{i\theta}\) と球面の回転 \(R_Z(\theta)\) の対応関係を図式で書くと次のようになる。\[
\begin{CD}
\Complex\cup\{\infty\} @> e^{i\theta} >> \Complex\cup\{\infty\} \\
@V \varphi VV @V \varphi VV \\
S^2 @> R_Z(\theta) >> S^2
\end{CD}
\]
というわけで、「\(e^{i\theta}\) 倍」という一次分数変換が球面の回転になっていることは分かった。では、球面の回転になるような一次分数変換は他にあるのか。あるいは、球面の回転にならない一次分数変換はあるのか。
今度は\[
\frac{z-1}{z+1}
\]という一次分数変換を考えてみよう。この変換によってリーマン球面の点がどう移るか、いくつか見てみると、\[
\begin{array}{ccc}
0&\mapsto&-1 \\
1&\mapsto&0 \\
-1&\mapsto&\infty \\
i&\mapsto&i \\
-i&\mapsto&-i \\
\infty&\mapsto&1
\end{array}
\]という感じになっている。図に表すと
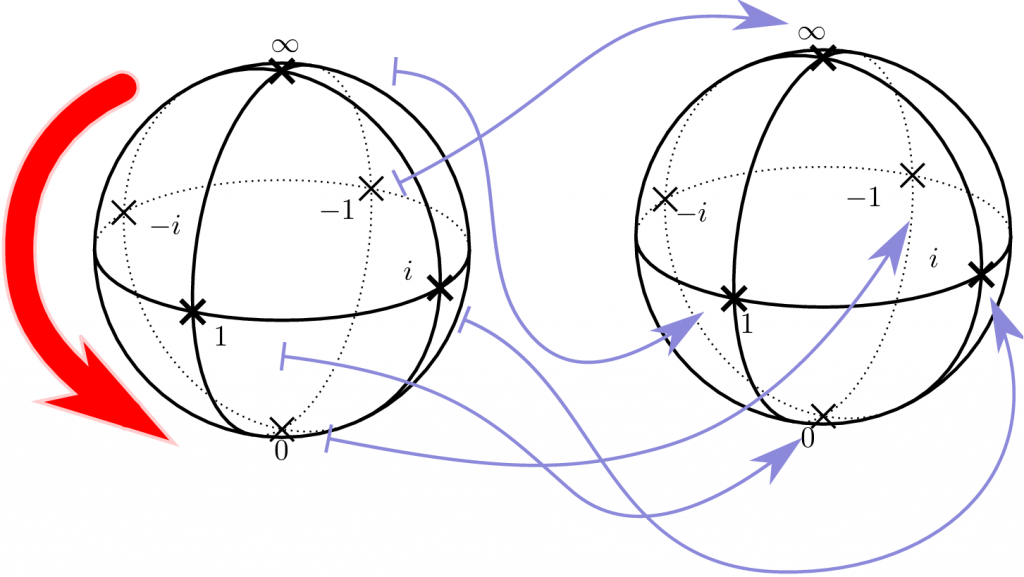
となる。これはどうも、\(i\) と \(-i\) を通る軸についての90°回転になっているようである。
一方、\[
z+1
\]という一次分数変換を考えると、これは \(\infty\) 以外の点を全て動かすので、回転ではない(回転を球面に作用させると動かない点が少なくとも2つある)。つまり、全ての一次分数変換が球面の回転という訳ではない。
では、どういう一次分数変換が球面の回転になっているのだろうか。逆に、球面の回転に対応する一次分数変換は必ず存在するのだろうか。
答えを先に言ってしまうと、特殊ユニタリ群 \(SU(2)\) で表される一次分数変換は常に球面の回転になる。逆に、球面の回転 \(SO(3)\) に対して必ず対応する一次分数変換があって、それは \(SU(2)\) で表される。
さっき見た「\(e^{i\theta}\) 倍」の一次分数変換が \(SU(2)\) の元の作用であることは、\[
\begin{pmatrix}e^{i\theta}&0\\0&1\end{pmatrix}\cdot z
=\frac{e^{i\theta}z+0}{0\cdot z+1}
=\frac{e^{i\theta/2}z+0}{0\cdot z+e^{-i\theta/2}}
=\begin{pmatrix}e^{i\theta/2}&0\\0&e^{-i\theta/2}\end{pmatrix}\cdot z
\]を見ると確かめられる。(\(\begin{pmatrix}e^{i\theta/2}&0\\0&e^{-i\theta/2}\end{pmatrix}\) は \(SU(2)\) の元である)
もう一つ見た \(\frac{z-1}{z+1}\) という変換についても、行列の作用として書くと\[
\begin{pmatrix}
1&-1\\
1&1
\end{pmatrix}\cdot z
=\frac{z-1}{z+1}
=\frac{\frac{1}{\sqrt{2}}z-\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}z+\frac{1}{\sqrt{2}}}
=\begin{pmatrix}
\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\
\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}
\end{pmatrix}\cdot z
\]という感じで \(SU(2)\) の作用として書ける。
図を描くのに疲れたので今回はここまで。図はInkscape+LATEXを使って頑張って描いた。
当初は複素射影直線 \(\Complex P^1=\{[z:w]\mid (z,w)\in\Complex^2,(z,w)\ne(0,0)\}\) を導入して議論しようかと思ったが話の流れがややこしくなりそうだったのでやめた。
