プログラミング言語Rustのα版が出たので遊んでみようかなという。(と言ってやってることはRustである必要性が全然ないけど)
ここで使っている環境はOS X 10.9.5 (アーキテクチャはx86_64)で、C++コンパイラはClangである。ここでやっているのは激しく環境依存なのだが、まあでもコンパイラがGCCかClangなら多くの環境で上手くいくんじゃないかと思う(知らん)。

明治維新で新政府がTeXを旧来の陋習として弾圧したとき、TeX使いたちはわざとTeXの使い勝手を悪くすることで難を逃れたと伝えられています。 — TeXしぐさ
↑「適当にでっち上げた嘘です」と注記しようと思ったが元ネタも適当にでっち上げた嘘だった
TeXの気に食わない点…はきっと皆さんいろいろあると思うが、ここではTeX処理系の挙動に絞った話をする。ここに書いた挙動に関しては、TeXもpdfTeXもXeTeXも大差はないようである。
次の形をした複素関数 \(f\) を一次分数変換という:\[
f(z)=\frac{az+b}{cz+d},\quad \text{ただし \(ad-bc\ne0\).}
\]分母が0になるとき(\(z=-d/c\) のとき)は \(f(z)\) の値は複素数としては定まらない、のだが、値が複素数であることにこだわらなければここは \(\infty\) としておくのが都合がいい。逆に、\(z=\infty\) のときは、(\(z\to\infty\) の極限を考えれば分かるように)\(f(z)\) の値は \(a/c\) として定義できそうである。何がいいたいかと言うと、一次分数変換は、複素平面の関数というよりは、複素平面に「無限遠点」を加えたもの \(\Complex\cup\{\infty\}\) の関数をみるのが自然である。
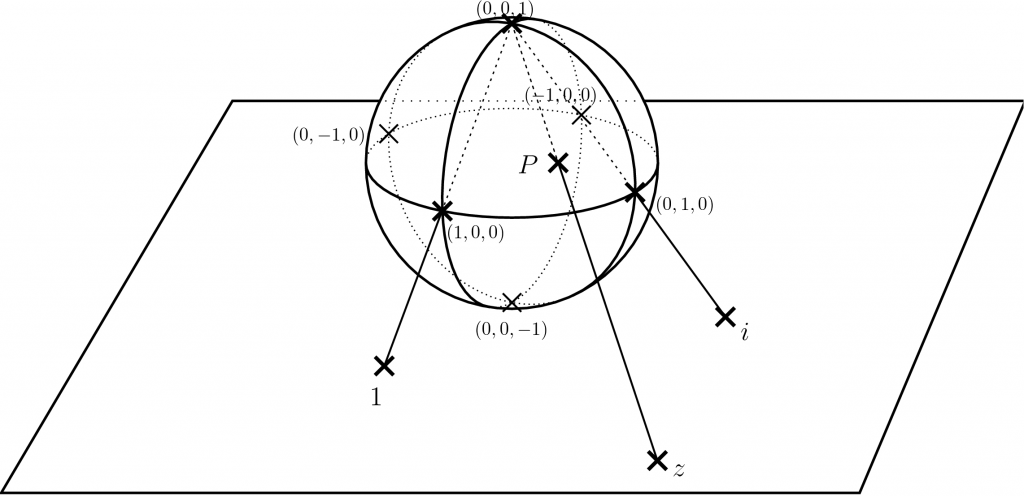
複素平面に無限遠点を加えたもの \(\Complex\cup\{\infty\}\) は、球面と同一視できる(こうやって同一視したものをリーマン球面という)。球面上の点 \(P\) に複素平面の点 \(z\) をどう対応させるかというと、球の北極 \((0,0,1)\) から \(P\) に直線を引いて、その直線が複素平面と交わる点 \(z\) を対応させる。逆に、複素平面の点 \(z\) に対しては、\(z\) と北極 \((0,0,1)\) を結ぶ直線を引いて、それが球面と交わる(北極じゃない方の)点 \(P\) を対応させる。北極に対応する点は複素平面上にはないので、北極には無限遠点 \(\infty\) を対応させる。この対応を立体射影(stereographic projection)という。
続きを読む
特殊直交群 \(SO(n)\) が(弧状)連結であることを示すのはこの記事に書いたやり方がおそらく正攻法なのだろうが、次元が低い時はもっと短い議論でできるんじゃないかなあと思った。
特殊ユニタリ群 \(SU(n)\) や特殊直交群 \(SO(n)\) が(弧状)連結であることは当たり前のようにバンバン使うけど自分でそらで証明できるか怪しいなあと思ったので、証明をつけてみることにした。
続きを読む
今回は \(\mathbf{R}^3\) のベクトル積とか回転行列とかに関する覚え書き。割と初等的。大学2年ぐらいのレベルだろうか。オチはない。
3次の実正方行列全体の集合を \(M(3,\mathbf{R})\) で表す。3次の特殊直交群 \(SO(3)\) を\[
SO(3)=\{A\in M(3,\mathbf{R})\mid\det A=1,~{}^tAA=I\}
\]で定める。特殊直交群の元はいわゆる回転を表す行列である。
3次の交代行列全体の集合を \(\mathfrak{so}(3)\) で表す。\(\mathfrak{so}\) は小文字のsoをフラクトゥールで書いたものである。\[
\mathfrak{so}(3)=\{X\in M(3,\mathbf{R})\mid X+{}^tX=0\}
\]\(\mathfrak{so}(3)\) は3次元の実線形空間であり、\begin{align*}
E_1&=\begin{pmatrix}0&0&0\\0&0&-1\\0&1&0\end{pmatrix},&
E_2&=\begin{pmatrix}0&0&1\\0&0&0\\-1&0&0\end{pmatrix},&
E_3&=\begin{pmatrix}0&-1&0\\1&0&0\\0&0&0\end{pmatrix}
\end{align*}は一組の基底となっている。\(\mathfrak{so}(3)\) の元 \(X\in\mathfrak{so}(3)\) は実数 \(a,b,c\in\mathbf{R}\) により\[
X=\begin{pmatrix}0&-c&b\\c&0&-a\\-b&a&0\end{pmatrix}=aE_1+bE_2+cE_3
\]と書ける。
(LaTeXではない方の)plain TeXを勉強すべしという電波を受信したので、勉強しようと思った。
じゃあ何を読んで勉強しようかという話だが、TeX Wiki内のTeX入門/マクロの作成 – TeX Wikiというページが入門として良さそうだった。
もうちょっとまじめに勉強しようとなると、TeXの本 – TeX Wikiの下の方にある
あたりを読むと良さそう。
11月22日から24日にかけて行われた東京大学駒場キャンパスでの第65回駒場祭で、数学科有志による「ますらぼ」企画(@UTmathlabo)に参加していました。「ますらぼ」では、数学科生・院生による発表、我々で作った冊子の配布、それから数学に関する展示が行われていました。
私は、かねてから作っていた複素関数を視覚化するWebアプリケーション “Conformality” に関する記事を書いたり、展示をしたりしていました。
冊子には、いくつかの複素関数の例・解説と、Webアプリの舞台裏に関する記事を書きました。一方、展示では、いくつかの複素関数の例・解説をポスター(というほどの紙の大きさでもない)で貼ったのと、パソコンとタブレットを用意して実際にWebアプリを動かしながら解説するのをやりました。
来場者に解説するとき、聞き手のレベルに合わせて話して、分かってもらうのは楽しかったです。実際どのぐらい理解してもらえたかは不明ですが…。あと、ふだんあまり喋らないので声が枯れました。
具体的に、レベルに応じてどんな内容を話したかというと、
小学生(!)
中学生
高校生
大学生
という感じでした。
教える関数としては、当初は一次分数変換が一番単純かなあと思いましたが、高校生を視野に入れるなら複素数のかけ算(拡大縮小と回転)からやった方が学習の役にも立つだろうと思って、冊子やポスターでは最初に複素数のかけ算の例を載せました。しかし、実際に人に教えるときはもっと初歩的な、複素数の足し算の幾何学的意味(平行移動)から始めたので、他人への解説の仕方というのは自分だけで考えてもわからないものだということを認識しました。
解説内容はそのうちこのブログかどこかに載せたいと思います(時間があれば)。
余談として、「ますらぼ」の教室では学内無線LANが使えないので、Webアプリケーションを動かすには工夫が必要でした。持ち込んだ機器は
で、MacでWebサーバーを動かしてWebアプリケーションを動かす感じにしました。URLは本来の “https://miz-ar.info/webapp/conformality/” で動いているように見せたかったので、MacBookとNexus 7で d-poppo.nazo.cc がMacBookのIPアドレスに解決されるようにしました。
ドメイン名に対して好き勝手なIPアドレスを割り当てるためには /etc/hosts をいじるのが手軽な方法だと思います。しかし、Androidの場合は /etc/hosts をいじるにはroot権限を取る必要があり、調べてみたところ思いの外危なそう&面倒くさそうだなあと思ったので、代わりに手元でDNSサーバーを動かすことにしました。MacBookにはDNSサーバーのソフトウエア(BIND9)が搭載されていた(最新のOSXにはないらしい)のですが、駒場祭直前にBIND9の使い方なんて覚えられない…。と思っていたらWebminとかいう便利なツールがあることを知ったので軟弱者の私はそれでBIND9を設定しました。めでたしめでたし。
最近のWindowsはタッチ操作に対応している。が、タッチに対応したディスプレイなんて持っておらず、わざわざ買うほど必要性も感じない。そういう場合に、iOS/Android端末と、リモートデスクトップ接続を受け付けることができるWindowsを持っていると、Windowsのタッチ操作を試せる。
今回のWindows 8.1を買う前の下調べで、(無印とProの違いの一つである)Windowsのリモートデスクトップ機能についてググっていたところ、「iOS/AndroidタブレットからリモートデスクトップでWindowsにつなぐと、タッチ操作ができる」という情報を見かけた(このへん)。そういうことなら、リモートデスクトップができるPro版を買うしかない。と思って、無印よりも数千円高いPro版のWindows 8.1を買ったのだった。
以下、iPadからリモートデスクトップでWindows機を操作するまでの手順。
コントロールパネルで
システムとセキュリティ > システム > リモートアクセスの許可
とクリック。
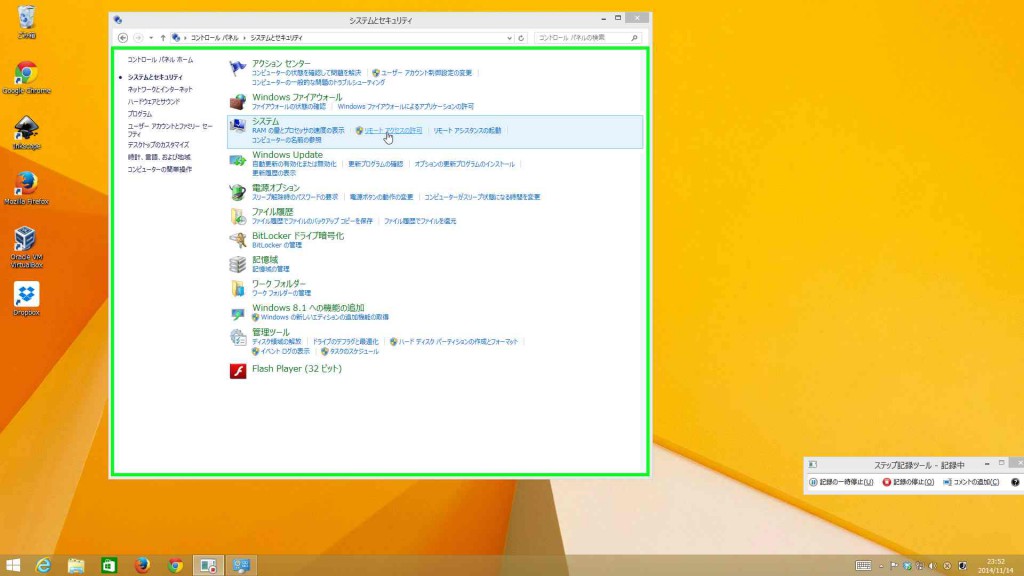
リモートデスクトップのオプションで、「このコンピューターへのリモート接続を許可する」をクリック。
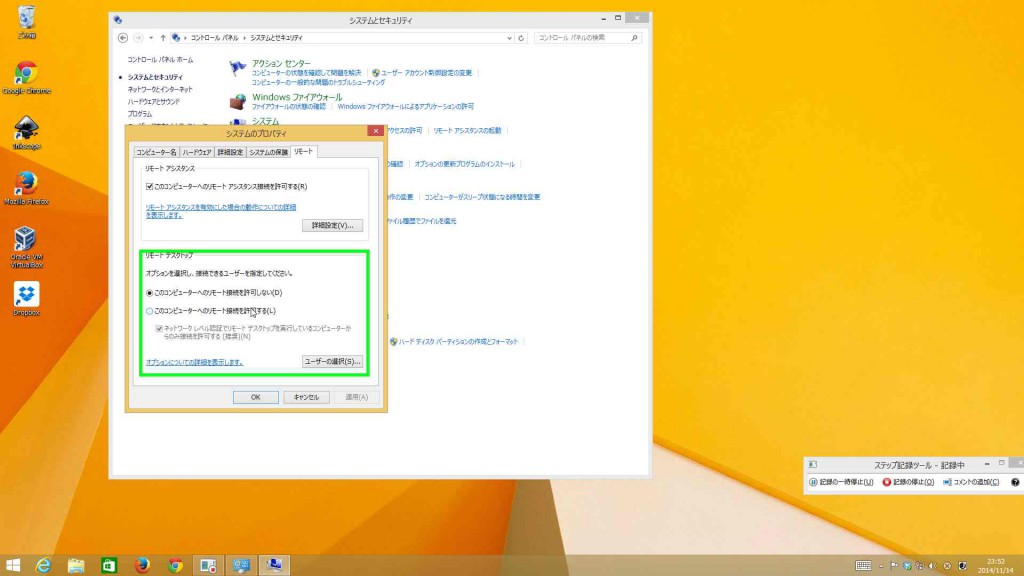
インストールが終わったら、起動して適当に設定してやる。
リモートデスクトップでつなぐと、画面サイズはクライアント側で指定したものになる。iPadからつなげばiPadの画面サイズになる。画面の向きは、横向きで固定のようだ。
「コンピューターの基本的な情報の表示」を見ると、「ペンとタッチ」の項目は「10タッチポイントでのタッチ(制限あり)のサポート」となっている。「制限あり」とあるがどこが制限されているのかはよく分からない。
みんな大好きな「ペイント」では、ブラシツールを使って複数点同時に描くことができるようだ。
SVGとはScalable Vector Graphicsの略で、2次元のベクター画像を記述するためのXMLベースの言語である。詳しくはググれ。
ベクター画像を構成する要素は、線分とか円とかベジエ曲線とかいろいろある。SVGでこれをどう表すかというと、例えば線分だとline要素を使い、円だとcircle要素を使う。SVGにはこの他にpath要素というものがあって、描画のコマンドを文字列で指定して複雑な曲線を描ける。線分とか円の弧のような単純なやつも描ける。
例を見てみると、
M 100 100 L 300 100 L 200 300 z
というコマンドを与えると、始点(100,100)から(300,100)に線分を描き、そこから続けて(200,300)に線分を描く。最後に、(200,300)から始点に線分を描いてパスを閉じる。この M とか L とか z とかいうのが描画コマンドで、それぞれ move to, line to, close path を意味する。2次元の描画を行うプログラムの経験がある人にはおなじみだろう。
描画コマンドには他にも2次あるいは3次のベジエ曲線を描くもの、楕円の弧を描くものがある。この楕円の弧を描くコマンド(A / a)が曲者で、楕円の指定方法が個性的だった。
このコマンドに与えるパラメーターは、楕円の形状に関する物が3つ、弧の終点(始点は current point を使うので、わざわざ指定する必要はない。指定したい場合は先に move to コマンドを実行する。)、そして、弧の端点と楕円の位置関係を指定するフラグが2つだ。楕円の中心は明示的に指定できない。
フラグが2つもある時点で嫌な予感がする。場合分けとか面倒くさそう。そんなことを感じながら、自前のSVGを出力するライブラリ(と言ったら大げさか)を実装・バグ取りしていたが、なぜか円全体が描けない。おかしい。と思ったが気が付いた。
始点と終点が一致していると、楕円の中心が一意に定まらない。つまり、SVG pathの A コマンドでは1回で楕円を描けない。SVGの楕円に類する物を描く描画コマンドは他にないのに…。
ググってみたら、Stack Overflowの質問を見つけた。
Circle drawing with SVG’s arc path – Stack Overflow
要するに、SVG pathで楕円全体を描くには、楕円の99.99%の弧を描いて満足するか、2個のコマンドで楕円を分割して描かないといけない。腐った仕様だ。
ちなみに、PostScriptの仕様をちらっと見た感じでは、PostScriptで円弧を描く arc コマンドは円の中心と半径、始点と終点の角度を指定する仕様だった。HTML5 Canvasの2D Contextも同様だ。(これらには楕円を描くコマンドはないが)