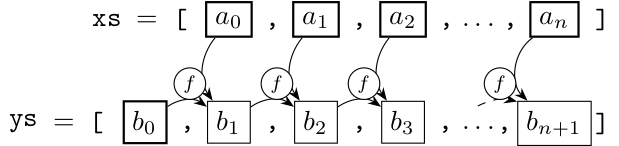
Haskellはリストを操作する関数を多数提供しています。map, filter, foldあたりが代表的で、これらは他の言語でもおなじみかと思います。
一方で、scan系関数（scanl, scanr）は他の言語ではあまり見かけない気がします。同じ関数型言語のSMLやOCamlにも標準では入っていないようです。
この記事では、scan系関数がどういう場合に利用できるかを紹介します。
続きを読む
Haskellのscan系関数を使いこなす
コメントを残す
「Haskell」カテゴリーアーカイブ
技術書典7に、Haskellで競技プログラミングをやる本を出します
今週末の9月22日（日）に池袋で開催される技術書典7に、新刊「Haskellで戦う競技プログラミング」を出します。既刊「LaTeX処理自動化ツールClutTeX 使い方とその仕組み」も改訂して紙の本を頒布します。
技術書典7について、公式サイトより引用：
日時 2019/09/22 (日) 11:00〜17:00
技術書典7
場所 池袋サンシャインシティ 展示ホールC/D（文化会館ビル2/3F）
主催 TechBooster/達人出版会
一般入場は11:00～13:00のみ有料です。詳細はこちら
気になる方はサークル詳細からチェックリストに入れてください：
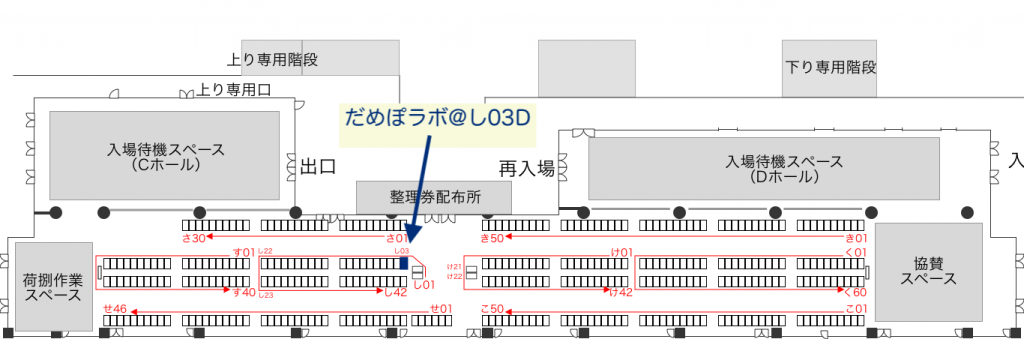
当サークルが配置されたのは「し03D」です。今回の技術書典は2Fの展示ホールDと3階の展示ホールCで行われますが、当サークルは2Fの展示ホールDです。会場が1箇所だった前回と同じ場所です。
Haskellでの浮動小数点数の方向付き丸めを考える
「週刊 代数的実数を作る」の #5 で、区間演算と方向付き丸めの話を書いた。浮動小数点数の計算は不正確だと思われがちだが、方向付き丸め等をうまく使えばある種の「正しい結果」（この数は確実に1.0より大きい、等）を得ることができる、という話だ。
MPFRのようなソフトウェア実装の浮動小数点数だと引数で丸めモードを指定できる。しかし、ハードウェア組み込み（注）の浮動小数点数（floatやdouble）の丸めモードを指定する方法は、言語や実行環境に依存する。
（注：環境によってはCPUに浮動小数点演算器が組み込まれておらず、floatやdoubleの演算もソフトウェア実装だったりするが、我々が普段使うPCではfloatやdoubleはほぼ確実にハードウェア実装されているため、以下「ハードウェア実装」で通す）
CやFortranのような低レベルかつ数値計算のニーズがあるようなプログラミング言語だと、丸めモードを変更する手段が用意されているが、JavaScriptやHaskellなど、そういうニーズが薄い言語では丸めモードの変更には対応していないことが多い。せいぜい、「浮動小数点数演算には最近接丸めを使用する」と規定されているのが関の山である。
しかし、「Haskellではできない処理がある」というのはどうにも気にくわない。どうにかして、ハードウェア組み込みの浮動小数点数の方向付き丸めをHaskellで扱う方法を考えたい。
ちなみに、ハードウェア組み込みの浮動小数点数にこだわらないのであれば、MPFRの丸めモード指定を使うHaskellライブラリーがすでに存在する：
http://hackage.haskell.org/package/rounded
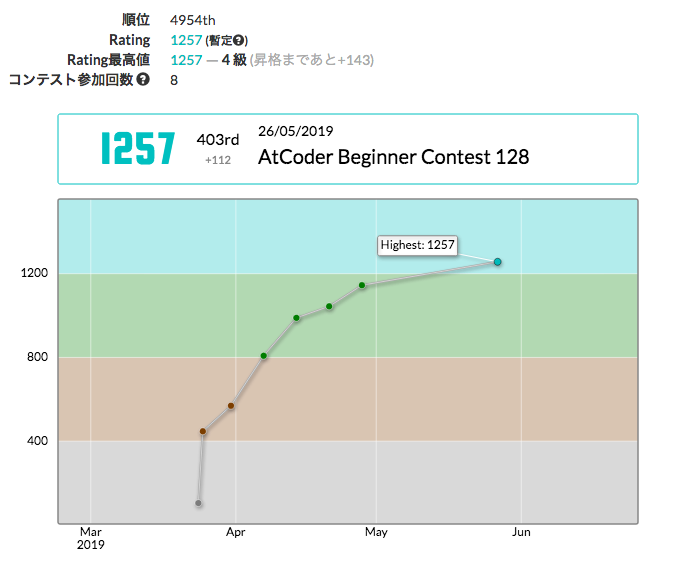
続きを読むHaskellでAtCoderに参戦して水色になった
3月下旬からAtCoderのRatedコンテストに参加しています（AtCoderプロフィール）。この度、5月26日のABC128でようやく水色になりました（AtCoder社長の記事によると、これは上位15%に相当するらしいです）。
使用言語はHaskellです。コンテストの時間中に提出したコードは全てHaskellだったと思います。
この記事では、Haskellを使う理由や、Haskellで競技プログラミングをするコツ、AtCoderでHaskellを使う際のアレコレなどを書いていきます。「水色になるための方法」みたいな話はしません（できません）。
続きを読むHaskellerのためのモノイド完全ガイド
Haskellにおけるモノイドについて解説記事を書いてみた。他の言語でも通用する話があるかもしれないし、ないかもしれない。
続きを読むフィボナッチ数絡みの競プロの問題を解いてみた（Typical DP Contest T）
この間、フィボナッチ数を計算する記事を書いていたら、@fetburner氏にこういう問題を教えて頂いた：
最速のフィボナッチ数計算を考える
Qiitaにこういう記事を書いた：
Haskellでフィボナッチ数列 〜Haskellで非実用的なコードを書いて悦に入るのはやめろ〜
↑の記事ではメモ化しない計算法が遅いこと、Haskellには遅延評価の罠があって正格にすると早くなること、「n番目のフィボナッチ数」をピンポイントで計算する場合は（行列またはQ(√5)の）冪乗を使う方法が早いこと、一般項（ビネの公式）をその辺の浮動小数点数で計算するのは使い物にならないこと、などを述べた。
まあ、「Haskellでは fib 0 = 0; fib 1 = 1; fib n = fib (n-1) + fib (n-2) でフィボナッチ数が計算できます！」に対する注意喚起としてはこれで十分すぎる内容なのだが、「n番目のフィボナッチ数をピンポイントで計算する方法」についてはもっと深掘りできる。
この記事では、数学的な考察も交えて、「n番目のフィボナッチ数をピンポイントで計算する方法」をより高速化してみたい。（計算量としてはどっちみち O(log n) くらいなのだが、定数倍の部分で高速化する）
なお、記事タイトルには「最速の」と書いたが、この記事で紹介するアルゴリズムが最速だと主張するわけではない（筆者の知らない、もっと早いアルゴリズムが存在するかもしれない）。 続きを読む
アプリカティブ関手ってなに？モノイド圏との関係は？調べてみました！
この記事は Category Theory Advent Calendar 2018 7日目 かつ Haskell (その2) Advent Calendar 2018 7日目の記事です。
Category Theory Advent Calendar 2018の6日目はcorollary2525さんの「随伴は あらゆるところに 現れる」、8日目は空席、9日目はt_uemura669101さんの「トポスと高階論理」です。
Haskell (その2) Advent Calendar 2018の6日目は空席、8日目はtakoeight0821さんの「Type defaultingについての初級的な解説」です。
この記事はどういう記事か
圏論の方から来た人向け：
デカルト積やテンソル積の一般化である「モノイド積」の話と、「内部ホム」の話をします。文献によっては内部ホムはモノイド積の右随伴として導入されますが、ここではモノイド構造を仮定せずに内部ホムの定式化（閉圏）をします。
Haskellの方から来た人向け：
この記事ではHaskellにおけるアプリカティブ関手の使い方は解説しません。Haskellの方から来た読者はすでにアプリカティブ関手をある程度知っており、圏論的な話にﾁｮｯﾄ興味がある、と仮定します。
これを読めば、「モナドは自己関手の圏におけるモノイド対象だよ、何か問題でも？」と同じノリで「アプリカティブ関手はモノイド圏における強laxモノイド関手だよ、何か問題でも？」と言って他人を煙に巻くことができます。 続きを読む
Haskell でのデバッグ手法あれこれ
プログラムにバグはつきものです。強力な型システムを備えている Haskell でもそれは同じです。この記事では、 Haskell プログラムのデバッグ手法をいくつか挙げてみます。
なお、使用している GHC は 8.2.2 です。より新しいバージョンで追加されるであろうより便利な機能は、この記事の対象外です。
Haskell で CGI を書く：Network.CGI（cgiパッケージ）
Haskell で CGI を書いてみよう。 続きを読む