最速のフィボナッチ数計算を考える

Qiitaにこういう記事を書いた：

Haskellでフィボナッチ数列〜Haskellで非実用的なコードを書いて悦に入るのはやめろ〜

↑の記事ではメモ化しない計算法が遅いこと、Haskellには遅延評価の罠があって正格にすると早くなること、「n番目のフィボナッチ数」をピンポイントで計算する場合は（行列またはQ(√5)の）冪乗を使う方法が早いこと、一般項（ビネの公式）をその辺の浮動小数点数で計算するのは使い物にならないこと、などを述べた。

まあ、「Haskellでは fib 0 = 0; fib 1 = 1; fib n = fib (n-1) + fib (n-2) でフィボナッチ数が計算できます！」に対する注意喚起としてはこれで十分すぎる内容なのだが、「n番目のフィボナッチ数をピンポイントで計算する方法」についてはもっと深掘りできる。

この記事では、数学的な考察も交えて、「n番目のフィボナッチ数をピンポイントで計算する方法」をより高速化してみたい。（計算量としてはどっちみち O(log n) くらいなのだが、定数倍の部分で高速化する）

なお、記事タイトルには「最速の」と書いたが、この記事で紹介するアルゴリズムが最速だと主張するわけではない（筆者の知らない、もっと早いアルゴリズムが存在するかもしれない）。

一般項（ビネの公式）による計算法を高速化する

フィボナッチ数列の一般項（ビネの公式）を再掲しておく。\[F_n=\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right)\]

この公式では \(\frac{1+\sqrt{5}}{2}\) の \(n\) 乗と \(\frac{1-\sqrt{5}}{2}\) の \(n\) 乗をそれぞれ計算して差を取っている。さて、「\(\frac{1+\sqrt{5}}{2}\) の \(n\) 乗」と「\(\frac{1-\sqrt{5}}{2}\) の \(n\)乗」は果たして、別々に計算する必要があるのだろうか？

浮動小数点数による計算の場合

\(\frac{1-\sqrt{5}}{2}\) は絶対値が1より小さい（\(-0.618\) くらい）ので、大きな \(n\) について \(n\) 乗するとほとんど 0 になる。よって、 \(n\) が大きい場合はこっちの項は無視して、\[\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n\]に最も近い整数を返せば良い。

ただ、浮動小数点数による計算ではそもそも \(n\) が大きい時に破綻するので、この最適化はあまり意味がない。

Q(√5) での計算の場合

\(\mathbf{Q}(\sqrt{5})\) の場合は「\(\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n\) に最も近い整数」を計算するというのが自明ではないので、浮動小数点数の場合と同じような方法は使えない。

だが、 \(\frac{1+\sqrt{5}}{2}\) と \(\frac{1-\sqrt{5}}{2}\) は \(\mathbf{Q}\) 上共役であり、その性質を使ってべき乗計算を1回で済ませることができる。

どういうことかというと、有理数 \(a_n\), \(b_n\) について\[\left(\frac{1+\sqrt{5}}{2}\right)^n=a_n+b_n\sqrt{5}\]とすると、\(\frac{1-\sqrt{5}}{2}\) の \(n\) 乗というのは \(\sqrt{5}\) の係数の符号を反転させた\[\left(\frac{1-\sqrt{5}}{2}\right)^n=a_n-b_n\sqrt{5}\]となる。これを使うと\[
\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right)
=\frac{(a_n+b_n\sqrt{5})-(a_n-b_n\sqrt{5})}{\sqrt{5}}
=2b_n
\]となり、つまり \(\frac{1+\sqrt{5}}{2}\) の \(n\) 乗の \(\sqrt{5}\) の係数を2倍したものが \(n\) 番目のフィボナッチ数、となる。（1月21日更新：数式の間違いを直した）

行列によるフィボナッチ数の計算を効率化する

フィボナッチ数の組に対してモノイド演算を定義する

今度は行列による方法の高速化を考えよう。

Qiita記事に書いた行列によるフィボナッチ数計算プログラムでは

data Mat2x2 a = Mat2x2 !a !a !a !a

というデータ型を定義してその \(n\) 乗を計算した。

だが、フィボナッチ数の計算という目的のために、成分が4つもある行列を使う必要があるのだろうか。一般項の計算に使った \(\mathbf{Q}(\sqrt{5})\) は有理数の成分が2つ、コード的には

data Ext_sqrt5 a = Ext_sqrt5 !a !a

だった。行列を使った計算法で4つも成分を使うのは冗長なように思える。

フィボナッチ数の計算に使う行列は \(\begin{pmatrix}0&1\\1&1\end{pmatrix}\) の \(n\) 乗という形だった。この形の行列が実際どのようなものになるか、いくつか見てみよう。\begin{align*}
\begin{pmatrix}0&1\\1&1\end{pmatrix}^1&=\begin{pmatrix}0&1\\1&1\end{pmatrix},\\
\begin{pmatrix}0&1\\1&1\end{pmatrix}^2&=\begin{pmatrix}1&1\\1&2\end{pmatrix},\\
\begin{pmatrix}0&1\\1&1\end{pmatrix}^3&=\begin{pmatrix}1&2\\2&3\end{pmatrix},\\
\begin{pmatrix}0&1\\1&1\end{pmatrix}^4&=\begin{pmatrix}2&3\\3&5\end{pmatrix},
\end{align*}

法則性が見えてきた。どうやら、\(\begin{pmatrix}0&1\\1&1\end{pmatrix}\) の \(n\) 乗、という行列は、フィボナッチ数 \(F_n\) を使って\[
\begin{pmatrix}0&1\\1&1\end{pmatrix}^n=\begin{pmatrix}F_{n-1}&F_n\\F_n&F_{n+1}\end{pmatrix}
\]と表せるようだ。実際、この関係式は簡単に証明できる（演習問題）。

この形の行列どうしの掛け算を考えると、\begin{align*}
\begin{pmatrix}F_{m+n-1}&F_{m+n}\\F_{m+n}&F_{m+n+1}\end{pmatrix}
&=\begin{pmatrix}0&1\\1&1\end{pmatrix}^{m+n} \\
&=\begin{pmatrix}0&1\\1&1\end{pmatrix}^m\begin{pmatrix}0&1\\1&1\end{pmatrix}^n \\
&=\begin{pmatrix}F_{m-1}&F_m\\F_m&F_{m+1}\end{pmatrix}\begin{pmatrix}F_{n-1}&F_n\\F_n&F_{n+1}\end{pmatrix} \\
&=\begin{pmatrix}F_{m-1}F_{n-1}+F_mF_n&F_{m-1}F_n+F_mF_{n+1}\\
F_mF_{n-1}+F_{m+1}F_n&F_mF_n+F_{m+1}F_{n+1}\end{pmatrix}
\end{align*}となるので、フィボナッチ数について\begin{align*}
F_{m+n-1}&=F_{m-1}F_{n-1}+F_mF_n,\\
F_{m+n}&=F_{m-1}F_n+F_mF_{n+1}=F_mF_{n-1}+F_{m+1}F_n,\\
F_{m+n+1}&=F_mF_n+F_{m+1}F_{n+1}
\end{align*}という関係式が得られる。

さらに、フィボナッチ数列の漸化式が \(F_{n+1}=F_n+F_{n-1}\) だったことを思い出せば、\begin{align*}
F_{m+n}&=F_mF_{n+1}+F_{m+1}F_n-F_mF_n,\\
F_{m+n+1}&=F_mF_n+F_{m+1}F_{n+1}
\end{align*}という2本の式が得られる。つまり、行列の乗算の代わりに\[(F_m,F_{m+1})\cdot(F_n,F_{n+1})\mapsto(F_mF_{n+1}+F_{m+1}F_n-F_mF_n,F_mF_n+F_{m+1}F_{n+1})\]という演算を使って計算できる。

一般の2×2行列どうしの掛け算の場合は乗算が8回と加算が4回必要だったが、「フィボナッチ数の計算に現れる行列」という性質を利用することで、乗算が4回（\(F_mF_n\)は2回登場するが、計算は1回で済む）と加算が3回に削減できたことになる。

\((F_n,F_{n+1})\) の形の組を FibPair と呼ぶことにすれば、 FibPair には\[(a,b)\cdot(a’,b’)\mapsto(a b’+ba’-aa’,aa’+bb’)\]によるモノイド演算（単位元は \((F_0,F_1)=(0,1)\)）が定まる（結合法則の確認は読者の演習問題とする）。Haskellでの実装例は次のようになる：

import Data.Semigroup
import Data.Monoid

-- FibPair a b : (a, b) = (F[n], F[n+1]) for some n
data FibPair a = FibPair !a !a deriving (Eq,Show)

instance (Num a) => Semigroup (FibPair a) where
  -- (F[m], F[m+1]) <> (F[n], F[n+1])
  --  ==> (F[m+n], F[m+n+1]) = (F[m] * F[n+1] + F[m+1] * F[n] - F[m] * F[n], F[m] * F[n] + F[m+1] * F[n+1])
  FibPair a b <> FibPair a' b'
    = FibPair (a * b' + (b - a) * a') (a * a' + b * b')
  stimes = stimesMonoid

instance (Num a) => Monoid (FibPair a) where
  -- (F[0], F[1])
  mempty = FibPair 0 1

-- fibOne = (F[1], F[2])
fibOne :: (Num a) => FibPair a
fibOne = FibPair 1 1

-- fibPair i = (F[i], F[i+1])
fibPair :: Int -> FibPair Integer
fibPair i = stimesMonoid i fibOne

fib :: Int -> Integer
fib i = case fibPair i of
          FibPair a _ -> a

ここで、 stimesMonoid は、モノイドの \(n\) 乗を \(n\) の二進展開を利用して高速に（O(log n)で）計算してくれる関数である（同様のアルゴリズムは、行列の \(n\) 乗の計算にも利用していた）。

このFibPairを使って123456789（およそいちおく）番目のフィボナッチ数を計算した場合と、一般の2×2行列の方法 (MatFib) での計算時間を比較してみる。

$ # 行列による計算
$ stack exec time fibonacci-hs-exe Mat atMod 123456789
F[123456789] === 4514 mod 10000
       9.28 real 8.84 user 0.33 sys

$ # FibPairによる計算
$ stack exec time fibonacci-hs-exe FibPair atMod 123456789
F[123456789] === 4514 mod 10000
       4.77 real 4.45 user 0.20 sys

FibPairは行列による計算のおよそ半分の時間で済んでいる。行列の方は演算1回あたり、多倍長整数の乗算が8回（と加算が4回）だったのに対し、FibPairの方は多倍長整数の乗算が4回で済むことが反映されていると考えられる。

せっかく「モノイド」という用語を出したので、整数とFibPairと2×2行列のモノイド構造の関係を図で表しておこう：

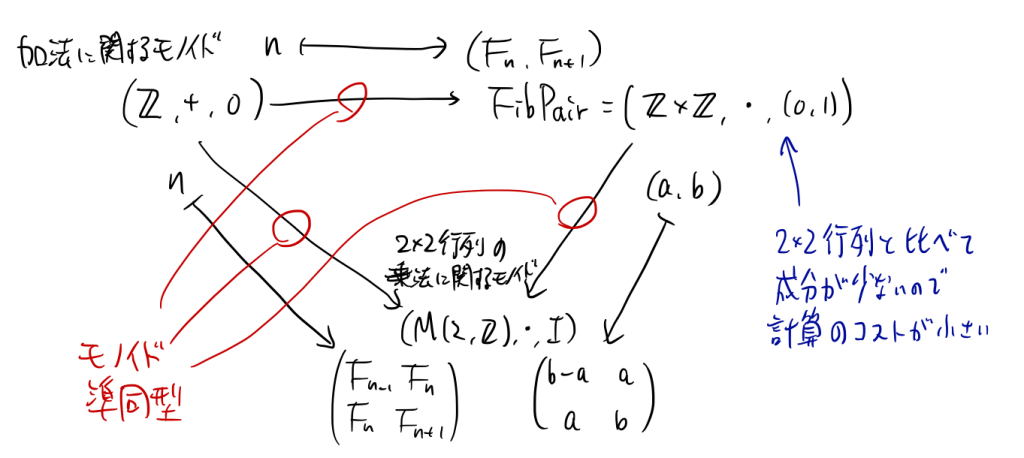整数 n に対して n 番目（および n+1 番目）のフィボナッチ数 \((F_n,F_{n+1})\) を対応させる写像は、整数の加法に関するモノイドから、FibPairへのモノイド準同型だとみなせる。

【2月3日追記】FibPairを一言で言うと、\(\mathbf{Z}[X]/(X^2-X-1)\)の乗法に関するモノイドである。詳しくはフィボナッチ数絡みの競プロの問題を解いてみた（Typical DP Contest T）の最後を参照。

Fast doubling

Haskellのべき乗 (^) やモノイドのn倍 stimesMonoid では、nを二進展開したものを「右から左に」辿って計算する、ということをやっている。

例えば、 a の19乗（二進法で10011）を計算したいというときは、アルゴリズム的には次のようなことを行なっている：

Y := 1, Z := a とおく。
n=19 の最下位ビット（1の位）は 1 なので、Y に Z をかける（Y := Y * Z）。
Z を自乗する（Z := Z * Z）。
n=19 の下から2番目のビット（2の位）は 1 なので、 Y に Z をかける（Y := Y * Z）。
Z を自乗する（Z := Z * Z）。
n=19 の下から3番目のビット（4の位）は 0 なので、 Y には何もしない。
Z を自乗する（Z := Z * Z）。
n=19 の下から4番目のビット（8の位）は 0 なので、 Y には何もしない。
Z を自乗する（Z := Z * Z）。
n=19 の下から5番目のビット（16の位）は 1 なので、 Y に Z をかける（Y := Y * Z）。
n は二進法で5桁なので、これでアルゴリズムを終了する。 Y は a の19乗である。

一つの式で書けば、\[a^{19}=a\cdot a^2\cdot (((a^2)^2)^2)^2\]と計算していることになるだろう。

さて、nを二進展開することによってn乗を計算する方法にはもう1通り、つまり「左から右に」辿る方法がある。

Y := 1 とおく。
n=19 の最上位ビット（16の位）は 1 なので、 Y に a をかける（Y := Y * a）。
Y を自乗する（Y := Y * Y）。
n=19 の上から2番目のビット（8の位）は 0 なので、 Y には何もしない。
Y を自乗する（Y := Y * Y）。
n=19 の上から3番目のビット（4の位）は 0 なので、 Y には何もしない。
Y を自乗する（Y := Y * Y）。
n=19 の上から4番目のビット（2の位）は 1 なので、 Y に a をかける（Y := Y * a）。
Y を自乗する（Y := Y * Y）。
n=19 の上から5番目のビット（2の位）は 1 なので、 Y に a をかける（Y := Y * a）。
n は二進法で5桁なので、これでアルゴリズムを終了する。 Y は a の19乗である。

一つの式で書けば、\[a^{19}=(((a^2)^2)^2\cdot a)^2\cdot a\]と計算していることになるだろう。

「右から左」と「左から右」の比較だが、計算機上では整数の二進表記を「右から左」に辿る方が実装しやすい（ひたすら2で割って、あまりを見れば良い）。そのため、「右から左」が使われることが多い。実際、Haskellのべき乗 (^) や stimesMonoid もそうなっている。

（二進表記の「右から左」と「左から右」のアルゴリズムについては、The Art of Computer Programming Vol. 2 に記載がある）

さて、「左から右」には、「右から左」にはない特徴がある。それは、アルゴリズム中で使う乗算が「自乗」と「a をかける」の2種類だけ、ということだ。この特徴と、フィボナッチ数計算 (FibPair) の事情を組み合わせるとどうなるか。

n乗のアルゴリズムをフィボナッチ数計算に使う場合、 a としては組 \(\operatorname{fibPair}(1)=(F_1,F_2)=(1,1)\) を用いる。そして、「a をかける」という操作は、「次のフィボナッチ数を計算する」ということであり、足し算1回でできてしまう：\[(F_n,F_{n+1})\cdot (1,1)=(F_{n+1},F_n+F_{n+1})\]「右から左」の場合は（自乗のほかに） FibPair の演算が3回必要だったところ、「左から右」なら多倍長整数の加算3回で済んでしまうのだから、「左から右」の方が有利である。

この「左から右」に辿る方法をフィボナッチ数に適用したものは、fast doubling と呼ばれているようだ。二進表記を「左から右」に辿るため、実装の際に末尾ではない再帰呼び出しを使うことになる。

Fast doubling をHaskellで実装すると次のようになる：

fastDoubling :: Int -> FibPair Integer
fastDoubling 0 = FibPair 0 1 -- (F[0], F[1])
fastDoubling 1 = FibPair 1 1 -- (F[1], F[2])
fastDoubling i                        -- let j := floor (i/2),
  = let p = fastDoubling (i `quot` 2) -- p = (F[j], F[j+1])
        q@(FibPair a b) = p <> p      -- q = (F[2j], F[2j+1])
    in if even i
       then q
       else FibPair b (a + b)         -- (F[2j+1], F[2j+2])

fib :: Int -> Integer
fib i = case fastDoubling i of
          FibPair a _ -> a

この時点ですでに FibPair + stimesMonoid よりも早くなっているが、いくつかの小細工を加えるとさらに早くなる。

まず、ここまできたらもはや FibPair の汎用的なモノイド演算は必要ない。モノイドとしての自乗 p <> p さえ計算できれば十分で、これは\[(a,b)\cdot(a,b)=(2ab-a^2,a^2+b^2)=(a(2b-a),a^2+b^2)\]で計算できる。モノイド演算では多倍長整数の乗算が4回、加減算が3回だったのが、自乗であれば多倍長整数の乗算が4回、加減算が2回となる。

fastDoubling :: Int -> FibPair Integer
fastDoubling 0 = FibPair 0 1 -- (F[0], F[1])
fastDoubling 1 = FibPair 1 1 -- (F[1], F[2])
fastDoubling i                                                  -- let j := floor (i/2), 
  = let FibPair a b = fastDoubling (i `quot` 2)                 -- (F[j], F[j+1])
        FibPair c d = FibPair (a * (2 * b - a)) (a * a + b * b) -- (F[2j], F[2j+1])
    in if even i
       then FibPair c d       -- (F[2j], F[2j+1])
       else FibPair d (c + d) -- (F[2j+1], F[2j+2])

そして、「FibPair を自乗してから次のフィボナッチ数を計算する」部分はひとまとめにできる。つまり、コード上は p <> p と FibPair b (a + b) に分かれていたのを、

fastDoubling :: Int -> FibPair Integer
fastDoubling 0 = FibPair 0 1 -- (F[0], F[1])
fastDoubling 1 = FibPair 1 1 -- (F[1], F[2])
fastDoubling i                                        -- let j := floor (i/2), 
  = let p@(FibPair a b) = fastDoubling (i `quot` 2)   -- (F[i/2], F[i/2+1])
    in if even i
       then FibPair (a * (2 * b - a)) (a * a + b * b) -- (F[2j], F[2j+1])
       else FibPair (a * a + b * b) (b * (2 * a + b)) -- (F[2j+1], F[2j+2])

とまとめることで多倍長整数の足し算を1回少なくできる。

最後に、これはどちらかというとGHCの最適化器の気まぐれによるところが大きそうだが、FibPair型をやめて普通のタプルを使うと若干早くなる。

fastDoubling :: Int -> (Integer, Integer)
fastDoubling 0 = (0, 1) -- (F[0], F[1])
fastDoubling 1 = (1, 1) -- (F[1], F[2])
fastDoubling i                               -- let j := floor (i/2), 
  = let (a, b) = fastDoubling (i `quot` 2)   -- (F[j], F[j+1])
    in if even i
       then (a * (2 * b - a), a * a + b * b) -- (F[2j], F[2j+1])
       else (a * a + b * b, b * (2 * a + b)) -- (F[2j+1], F[2j+2])

fib :: Int -> Integer
fib i = case fastDoubling i of
          (a, _) -> a

実験（実行時間の計測）

筆者の環境（MacBook Pro (Late 2013), GHC 8.6.3）では、行列を使った版で123456789番目のフィボナッチ数を計算したところ11秒程度、FibPairとstimesMonoidを使った版で同じ計算をしたところ5秒程度、fast doublingを使った版（最後に載せた、タプルを使ったコード）では1.7秒程度かかった。

$ git clone https://github.com/minoki/fibonacci-hs.git
$ cd fibonacci-hs
$ stack build
$ stack exec time fibonacci-hs-exe Mat atMod 123456789
F[123456789] === 4514 mod 10000
       10.74 real 9.51 user 0.42 sys
$ stack exec time fibonacci-hs-exe FibPair atMod 123456789
F[123456789] === 4514 mod 10000
        5.42 real 4.76 user 0.25 sys
$ stack exec time fibonacci-hs-exe FastDoubling atMod 123456789
F[123456789] === 4514 mod 10000
        1.69 real 1.56 user 0.08 sys

なお、記事の最初の方で書いた、一般項を \(\mathbf{Q}(\sqrt{5})\) で計算するやつ（\(\left(\frac{1+\sqrt{5}}{2}\right)^n\) の計算だけで済ませる）は、5秒程度だった。こちらは有理数計算を伴うため、整数演算のみのFastDoublingには勝てないのだろう（推測）。

$ stack exec time fibonacci-hs-exe BinetSqrt5Half atMod 123456789
F[123456789] === 4514 mod 10000
        4.80 real 4.54 user 0.20 sys

結論として、この記事で触れたアルゴリズムの中では fast doubling が一番早い。

実験用のソースコードは https://github.com/minoki/fibonacci-hs に置いてある。

おまけ：多倍長計算の特性を考慮する

FibPairの演算には\[(F_mF_{n+1}+F_{m+1}F_n-F_mF_n,F_mF_n+F_{m+1}F_{n+1})\]という式が登場したが、コード例では分配法則を使って\[(F_mF_{n+1}+(F_{m+1}-F_m)F_n,F_mF_n+F_{m+1}F_{n+1})\]に相当する式を計算した。Haskellコードで書けば

 let aa' = a * a' in FibPair (a * b' + b * a' - aa') (aa' + b * b') -- A

と

FibPair (a * b' + (b - a) * a') (a * a' + b * b') -- B

である。これら（前者をA、後者をBと呼ぶことにする）は数学的には等価だが、実際にコーディングする際はどちらを使うべきだろうか。

演算回数でいうと、A, B どちらも乗算が4回、加減算が3回ずつである。では、どちらを使っても同じなのだろうか。この辺の話は、演算対象となる型によって変わってくる。

固定長整数型や固定長浮動小数点数は、オペランドの範囲に関わらず演算の速度は一定だと考えられる。つまりAとBどちらを採用しても同じである。一方、多倍長整数は、オペランドの桁数が多いほど演算に時間がかかる。したがって、AとBで実行時間に差が出てくる可能性がある。

仮に、変数 a, a', b, b' のいずれもn桁の整数だとしよう。すると、Aの方は

n桁の整数同士の乗算が4回
2n桁の整数同士の加減算が3回

なのに対し、Bの方は

n桁の整数同士の乗算が4回
2n桁の整数同士の加減算が2回
n桁の整数同士の加減算が1回

と、加減算1回分について、2n桁とn桁の違いがある。2n桁とn桁ではn桁の方が早いので、多倍長で計算する際はBの方を採用すべきだと考えられる。

余談：HaskellのSemigroup/Monoidには自乗するためのメソッドがない

（1月21日追記）

モノイドの元のn乗を計算する際、「左から右」「右から左」のいずれも、モノイドの元の自乗 \(x^2\) の計算を利用した。Data.SemigroupやData.Monoidには積を計算するメソッド <> はあるが、自乗に特化されたメソッドはないので、自乗の計算には積演算 <> が使われることになる。

自乗に特化されたメソッドがあると何が嬉しいかというと、インスタンスによっては一般の積演算 <> よりも高速な実装を提供できる可能性があり、 stimesMonoid のような関数がそれを利用できるようになることである。sconcat や stimes がクラス外の関数ではなくて Semigroup クラスの中で定義されているのと同じ理由である。もちろん「自乗するメソッド」のデフォルト実装は \x -> x <> x とする。

コードで書けば、 Semigroup クラスがこういう風に定義されていてほしい：

class Semigroup a where
  (<>) :: a -> a -> a
  sconcat :: NonEmpty a -> a -- 連結
  sconcat = ...
  stimes :: Integral b => b -> a -> a -- n倍するメソッド
  stimes = ...
  twice :: a -> a -- 自乗するメソッド
  twice x = x <> x

FibPairの場合に、この「自乗する」 twice メソッドがあるとどの程度嬉しいか。FibPairのモノイド演算は次のように定義されていた：

 FibPair a b <> FibPair a' b' = FibPair (a * b' + (b - a) * a') (a * a' + b * b')

この演算では多倍長整数の乗算を4回、多倍長整数の加減算を3回行う。

一方、FibPairの自乗は次のように計算できる：

twice (FibPair a b) = FibPair (a * (2 * b - a)) (a * a + b * b)

（fast doublingの説明で同じことを書いたが）こちらは多倍長整数の乗算が4回、多倍長整数の加減算が2回で、加減算が1回減った上に乗算1回分が定数 2 の掛け算に変わっている。

よって、多倍長整数でFibPairを計算する際は、一般のモノイド演算よりも自乗に特化したコードを使った方が真に早い。

先ほどリンクを貼った実験プログラムでは、 FibPair の自乗で特化したコードを使うようにしたものを FibPairX という名前（名付けが雑だ）で実装しており、それぞれ234567890番目のフィボナッチ数を計算させてみると

$ stack exec time fibonacci-hs-exe FibPair atMod 234567890
F[234567890] === 2145 mod 10000
        9.87 real 9.34 user 0.38 sys
$ stack exec time fibonacci-hs-exe FibPairX atMod 234567890
F[234567890] === 2145 mod 10000
        9.33 real 8.76 user 0.41 sys

という風に FibPairX の方が若干早い。

（このことから、GHCの最適化器は \x -> x <> x というコードを式変形して上記の twice の実装に変えるようなことは行わない、ということがわかる。数学的に同値な式でも多倍長整数のコストを考えると優劣があるのは「おまけ：多倍長計算の特性を考慮する」で見た通りなので、コンパイラーが勝手にそういう式変形を行わないことはプログラマーにとっては生成コードを予測できるということであり、良いことなのだが。）

というわけで、HaskellのSemigroupクラスに自乗に特化したメソッドがあるといいなあ〜〜、という話でした。

まとめ

一般項による計算は、べき乗の計算を1回で済ませることができる。
行列によるフィボナッチ数の計算は高速だが、登場する行列に冗長性（成分の間の関係式）があるので、それを利用してさらなる最適化（2倍程度）ができる。
- 数学チックに言えば、空間の次元を落としている（4から2）
二進展開を「右から左」ではなく「左から右」に変え、フィボナッチ数の事情も組み合わせることで、さらに高速化ができる。その結果得られるアルゴリズムは、 fast doubling と呼ばれている。
数学のちからはすごいぞ！！（ツッコミ禁止）

雑記帳

人生やっていき