逆双曲線関数と逆三角関数をナメてかかっていたら落とし穴にはまったので、ブログ記事としてまとめておく次第である。 続きを読む
逆双曲線関数と逆三角関数の branch cut
1件のフィードバック
「数学」カテゴリーアーカイブ
たのしい複素積分
1年近く前に、複素積分をインタラクティブに行える Web ページ（Web アプリ？）を作ったのだが、ブログでの紹介がまだだった。
0の0乗
「0の0乗」については、数学をやっている人とそうじゃない人で割と認識に差がありそうだと思う。そこで、（まだ青二才の学生ではあるが）数学をやっている者の端くれとして思うことを書いておく。
まず、（たぶん）世間でよく言われている「0の0乗を1とすべき理由」と「0の0乗が不定となる理由」について述べ、それを踏まえて、数学をやる上での「それでも0の0乗を1とする理由」を述べる。 続きを読む
豊穣圏の教科書
最近、豊穣圏(enriched category)という概念に触れることがあって、それの標準的な教科書って何かなあと思ったら、G.M.Kelly “Basic Concepts of Enriched Category Theory”というのがそれっぽくて、しかも無料でPDFをダウンロードできるらしい。
MacLaneのCWMには豊穣圏の名前といくつかの例は出てくるけどちゃんとした定義は出てこない。まあ、ちゃんとした定義を書こうとするとモノイド圏(monoidal category)の定義をしてうんたらしないといけないようだが。
豊穣圏というのは（今の自分の理解で）大雑把に言うと、圏のhom-setに単なる「集まり」以上の構造が入ったものである。例えば、加群の圏には、それぞれのhom-setにアーベル群の構造が入っているので、アーベル群の圏 Ab でenrichされた圏の例となっている。
別の例を挙げると、各hom-setにゼロ射が入っている圏は、それぞれのhom-setに点つき集合の構造（ゼロ射が基点）が入っているとみなせる。つまり、ゼロ射を持つ圏は、点つき集合の圏 Set* でenrichされた圏と言える。
各hom-setに構造が入っていればいいというものではなくて、Ab-enriched categoryだと射の合成が双線形、Set*-enriched categoryだとゼロ射（hom-setの基点）を合成するとゼロ射、という風に、合成の方にも条件が付いてくる。この辺の条件を表現するのに、モノイド圏の構造が必要になる。
ガンマ関数の計算（Lanczos近似）
ガンマ関数とは、みなさんおなじみの、
- \(\Gamma(z+1)=z\Gamma(z),\)
- \(\Gamma(1)=1,\)
- \(x>0\) に対し \(\log\Gamma(x)\)は凸
を満たす \(\def\Complex{\mathbf{C}}\Complex\) 上の有理型関数である。\(\DeclareMathOperator\Re{Re}\Re z>0\) に対しては、以下の積分表示がある。\[
\Gamma(z)=\int_0^\infty t^{z-1}e^{-t}dt
\]
階乗 \(n!\) との関係は\[
n!=\Gamma(n+1)
\]となる。
重要な公式としては、反転公式\[
\Gamma(1-z)\Gamma(z)=\frac{\pi}{\sin\pi z}
\]がある。特に、\(z=\frac{1}{2}\) とおけば \(\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}\) が得られる。
さて、コンピューターでガンマ関数の値を数値的に計算するにはどうすればいいのか。指数関数とか三角関数だとかは分かりやすい冪級数表示があったから良かったが、ガンマ関数にはそういうのはないのか。
いろいろググって調べた結果、ガンマ関数の近似方法として、Lanczos近似というのがあるらしい。が、ググっているだけではいまいちその実体が釈然としないし、導出方法もよくわからない。なので、Lanczosの原論文（1964）を読むことにした。大学院生という身分は便利なもので、大学の図書館でその論文にアクセスできた。
東大入試理系数学2015第5問（解いてみた）
一次分数変換と球面の回転の話(0)
次の形をした複素関数 \(f\) を一次分数変換という:\[
f(z)=\frac{az+b}{cz+d},\quad \text{ただし \(ad-bc\ne0\).}
\]分母が0になるとき（\(z=-d/c\) のとき）は \(f(z)\) の値は複素数としては定まらない、のだが、値が複素数であることにこだわらなければここは \(\infty\) としておくのが都合がいい。逆に、\(z=\infty\) のときは、（\(z\to\infty\) の極限を考えれば分かるように）\(f(z)\) の値は \(a/c\) として定義できそうである。何がいいたいかと言うと、一次分数変換は、複素平面の関数というよりは、複素平面に「無限遠点」を加えたもの \(\Complex\cup\{\infty\}\) の関数をみるのが自然である。
複素平面に無限遠点を加えたもの \(\Complex\cup\{\infty\}\) は、球面と同一視できる（こうやって同一視したものをリーマン球面という）。球面上の点 \(P\) に複素平面の点 \(z\) をどう対応させるかというと、球の北極 \((0,0,1)\) から \(P\) に直線を引いて、その直線が複素平面と交わる点 \(z\) を対応させる。逆に、複素平面の点 \(z\) に対しては、\(z\) と北極 \((0,0,1)\) を結ぶ直線を引いて、それが球面と交わる（北極じゃない方の）点 \(P\) を対応させる。北極に対応する点は複素平面上にはないので、北極には無限遠点 \(\infty\) を対応させる。この対応を立体射影(stereographic projection)という。
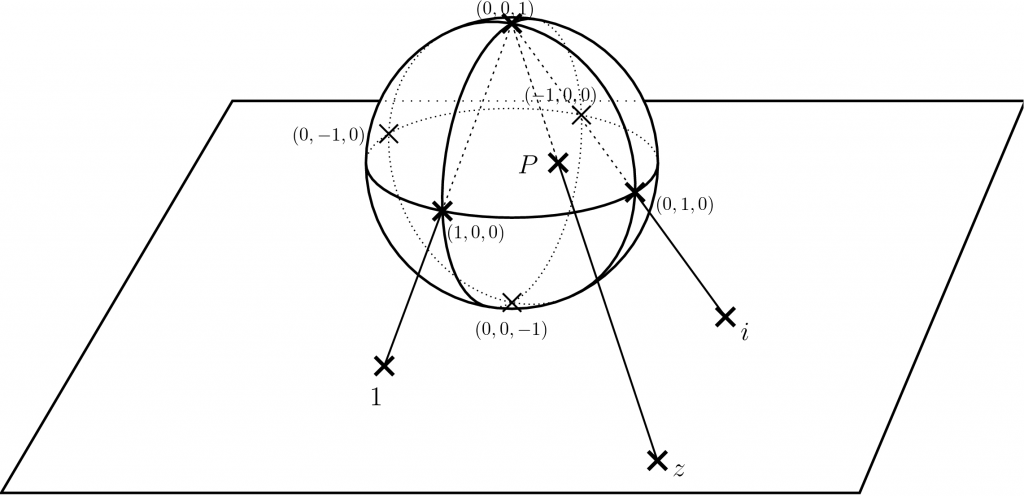
続きを読む
SO(2) と SO(3) が弧状連結であることの簡便な（？）証明
特殊直交群 \(SO(n)\) が（弧状）連結であることを示すのはこの記事に書いたやり方がおそらく正攻法なのだろうが、次元が低い時はもっと短い議論でできるんじゃないかなあと思った。
命題. \(SO(2)\) の元 \(A\) は次の形に書ける。\[
A=\begin{pmatrix}
\cos\theta&-\sin\theta \\
\sin\theta&\cos\theta
\end{pmatrix}
\]
A=\begin{pmatrix}
\cos\theta&-\sin\theta \\
\sin\theta&\cos\theta
\end{pmatrix}
\]
証明. \(A\) を成分表示して \(SO(2)\) の条件の式に代入してガリガリ計算すればわかる。
定理. \(SO(2)\) は弧状連結である。
証明. さっきの命題を使えば簡単。
SU(n) と SO(n) が弧状連結であることの証明
特殊ユニタリ群 \(SU(n)\) や特殊直交群 \(SO(n)\) が（弧状）連結であることは当たり前のようにバンバン使うけど自分でそらで証明できるか怪しいなあと思ったので、証明をつけてみることにした。
続きを読む
R^3のベクトル積とso(3)のメモ
今回は \(\mathbf{R}^3\) のベクトル積とか回転行列とかに関する覚え書き。割と初等的。大学2年ぐらいのレベルだろうか。オチはない。
定義とか
3次の実正方行列全体の集合を \(M(3,\mathbf{R})\) で表す。3次の特殊直交群 \(SO(3)\) を\[
SO(3)=\{A\in M(3,\mathbf{R})\mid\det A=1,~{}^tAA=I\}
\]で定める。特殊直交群の元はいわゆる回転を表す行列である。
3次の交代行列全体の集合を \(\mathfrak{so}(3)\) で表す。\(\mathfrak{so}\) は小文字のsoをフラクトゥールで書いたものである。\[
\mathfrak{so}(3)=\{X\in M(3,\mathbf{R})\mid X+{}^tX=0\}
\]\(\mathfrak{so}(3)\) は3次元の実線形空間であり、\begin{align*}
E_1&=\begin{pmatrix}0&0&0\\0&0&-1\\0&1&0\end{pmatrix},&
E_2&=\begin{pmatrix}0&0&1\\0&0&0\\-1&0&0\end{pmatrix},&
E_3&=\begin{pmatrix}0&-1&0\\1&0&0\\0&0&0\end{pmatrix}
\end{align*}は一組の基底となっている。\(\mathfrak{so}(3)\) の元 \(X\in\mathfrak{so}(3)\) は実数 \(a,b,c\in\mathbf{R}\) により\[
X=\begin{pmatrix}0&-c&b\\c&0&-a\\-b&a&0\end{pmatrix}=aE_1+bE_2+cE_3
\]と書ける。