Haskellはリストを操作する関数を多数提供しています。map, filter, foldあたりが代表的で、これらは他の言語でもおなじみかと思います。
一方で、scan系関数(scanl, scanr)は他の言語ではあまり見かけない気がします。同じ関数型言語のSMLやOCamlにも標準では入っていないようです。
この記事では、scan系関数がどういう場合に利用できるかを紹介します。
目次
scan系関数とは
定義と図解
scan系関数は、リストを元にして新しいリストを構築する関数です。新しいリストの要素は、与えられた初期値と関数を使って元のリストを途中まで畳み込んだものになります。「foldの途中経過を残す版」とでも言えば良いでしょうか。
型はそれぞれ次のようになります:
scanl :: (b -> a -> b) -> b -> [a] -> [b]
scanr :: (a -> b -> b) -> b -> [a] -> [b]
どちらも第一引数は関数(二項演算と思っても良いでしょう)、第二引数は初期値、第三引数は元になるリストです。foldと同じです。比較のためにfoldの型も載せておきます:
foldl :: (b -> a -> b) -> b -> [a] -> b
foldr :: (a -> b -> b) -> b -> [a] -> b
scan系関数の動作については、言葉や式で説明するよりも、図を使った方がわかりやすいかもしれません。元のリストを xs, 初期値を \(b_0\) または \(b_{n+1}\), 関数(二項演算)を \(f\) とした時に scanl または scanr が構築するリストは、次の図のようになります:
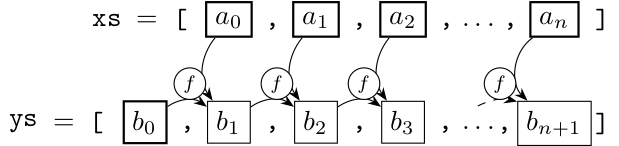
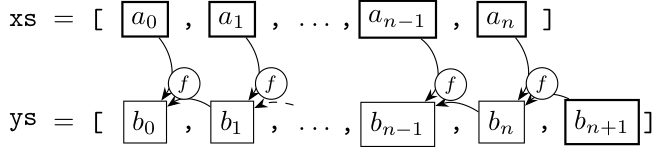
式で書くと、scanlの方は\[b_{k+1}=f(b_k,a_k),\]scanrの方は\[b_k=f(a_k,b_{k+1})\]となります。
HaskellのPreludeにはリスト用のscanl, scanrが用意されているほか、Data.VectorにはVector版のscanl, scanrが定義されています。
遅延評価のサンクを溜めたくない人は、例によってプライムがついた scanl', scanr' が Data.List からエクスポートされているのでそれを使うと良いでしょう。
foldとの関係
scanlの返すリストの末尾の要素は、同じ引数(関数、初期値、リスト)についてfoldlを適用した結果と同じです。同様に、scanrの返すリストの先頭はfoldrの結果と同じです。Haskellコードで書くと次のような関係が成り立っています:
last (scanl f z xs) == foldl f z xs
head (scanr f z xs) == foldr f z xs
違いは、scan系関数が「途中結果も残している」という点です。
なお、fold系関数は演算子に応じて sum, productやmaximum, minimum, and, orなどの特化された関数が用意されていますが、scan系関数にはそういう特化された関数は用意されていません。
利用例
筆者が競プロをする中で遭遇したscan系関数の使いどころを挙げていきます。例示するコードはリストをscanしていますが、実際に提出するコードは効率のことを考えてVectorを使っています。また、競プロではどうせunboxed vectorを使うので scanl と scanl' の違いはありません。なので、タイプ数節約のためにプライム ' のつかない方を原則として使います。
階乗のリスト
Haskellで階乗を計算するには product [1..n] と書くのはみなさん知っていますね。product 関数と等差数列の記法が組み合わさって非常にエレガントです。
階乗の値が1回しか必要ないという場合はこれで良いのですが、階乗や二項係数をたくさん使う問題の場合、「n以下の整数の階乗」をあらかじめ計算しておくと便利です。あらかじめ計算しておけば、二項係数なら以下のように計算できます:
binom :: Int -> Int -> Integer
binom n k = factList !! n `div` (factList !! (n - k) * factList !! k)
(リストを使うと要素へのアクセスで結局時間がかかってしまいますが、実際の提出コードではVectorを使うので定数時間になります)
scanl関数を使うと、階乗のリスト(ベクター)を1行で定義することができます。つまり、 \(0!\) から \(1000!\) までが入ったリストを作る関数を次のように実装できます:
factList :: Integer -> [Integer]
factList = scanl (*) 1 [1..1000]
-- factList = [1,1,2,6,24,120,...]
実際の競技プログラミングでは階乗の値は Integer としてではなく、\(10^9+7\)などの法で割った余りが必要になることが多いでしょう。その場合は、型を IntMod 型みたいなものにするか、乗算を (*) ではなく mulMod のような関数にすることになるでしょう。
ところで、最初に書いた product [1..n] は、fold系関数を使うと foldl (*) 1 [1..n] と書けます。さっき定義した factList は foldl (*) 1 [1..n] の foldl を scanl に置き換えたものになっています。fold系関数が「最終結果 \(n!\) だけを残す」のに対してscan系関数が「途中結果 \(0!\), \(1!\), \(2!\), …, \((n-1)!\), \(n!\) も残す」という対比がわかりやすいかと思います。

累積和、累積GCD、累積xor
整数のリスト \([a_0,a_1,\ldots,a_n]\) が与えられた時、その累積和 \begin{align*}b_0&:=0,\\b_1&:=0+a_0,\\b_2&:=0+a_0+a_1,\\&\vdots\\b_{n+1}&:=0+a_0+a_1+\cdots+a_n\end{align*}を計算したいという状況がよくあります。例えば、様々な \(i\), \(j\) について部分和 \(a_i+\cdots+a_j\) を計算する必要がある場合、事前に累積和を計算しておけば \(a_i+\cdots+a_j=b_{j+1}-b_i\) と計算できます。
累積和もscan系を使えば一発で計算できます。左から順に和を計算する場合は scanl を、右から計算する場合は scanr を使います。計算例を挙げておきます:
scanl (+) 0 [2,0,1,9] == [0,2,2,3,12]
scanr (+) 0 [2,0,1,9] == [12,10,10,9,0]
累積「和」の部分を他の演算に代えてやって、初期値を単位元っぽいものにしてやれば、他の累積リストも作れます。例えばmaxと最小値を使えば「累積max」が、xorと0を使えば「累積xor」を作れます。累積maxとは「先頭からn番目までの最大値」が入ったリストのことですね。
変わり種として、「累積GCD」が話題になったことがありました。非負整数のGCDをモノイド演算と見たときの単位元は0なので、 scanl gcd 0 xs という感じで使うことになります。
一点を除いた部分の和を取る
列 \(a_0,a_1,\ldots,a_n\) があった時に、各\(a_i\)を取り除いた時のGCDや最大値を求めたい場合があります。\[\gcd(a_0,a_1,a_2,\ldots,a_{i-1},a_{i+1},\ldots,a_n)\]みたいなやつです。取り除く\(i\)が一種類だけなら普通に計算すれば良いのですが、全ての\(i\)に対してそれを取り除いた総和(和ではないけど…)を計算するとなると大変です。さっきリンクを貼った ABC125-C はまさにこの種の問題です。素朴にやると\(O(n^2)\)の時間がかかってしまいます。
足し算のように可逆な演算であれば総和を計算してから取り除きたい値を引けば効率的に計算できますが、GCDや最大値の場合はそうはいきません。しかし、scanlで「累積GCD」や「累積max」を計算すれば効率よく(\(O(n)\)で)計算できます。
具体的には、計算したい「1箇所取り除いた総和(和ではない)」を\[\gcd(a_0,a_1,a_2,\ldots,a_{i-1},a_{i+1},\ldots,a_n)=\gcd(\gcd(a_0,a_1,a_2,\ldots,a_{i-1}),\gcd(a_{i+1},\ldots,a_n))\]と分解します。分解した後の\(\gcd(a_0,a_1,\ldots,a_{i-1})\)と\(\gcd(a_{i+1},\ldots,a_n)\)はそれぞれ左からの累積GCDと右からの累積GCDなので、scan系関数で計算できます。
処理としては scanl と scanr 関数をそれぞれ計算し、 zipWith で組み合わせる感じになります。この際、zipWith gcd (scanl gcd 0 xs) (scanr gcd 0 xs) と書いてしまうと「元の列全体のGCD」を\(n+1\)個複製したリストになってしまうので、 zipWith gcd (scanl gcd 0 xs) (tail $ scanr gcd 0 xs) という風に適宜 tail を噛ませてずらしておきます。
この手の問題をいくつか挙げておきます。
- AtCoder Beginner Contest 125 C – GCD on Blackboard
- GCDについて
- AtCoder Beginner Contest 134 C – Exception Handling
- 最大値について
ここまでに紹介した例では、scan系関数に渡す関数と初期値は、何らかのモノイド(二項演算と単位元)になっていました。(「モノイド」という言葉に馴染みのない方は「Haskellerのためのモノイド完全ガイド」を読んでください)
ここからは、モノイドではない例を挙げていきます。
動的計画法に使う
ある種の動的計画法をscan系関数を使って書ける場合があります。
例としては、この間出した同人誌「Haskellで戦う競技プログラミング」のLCSで使いました。詳しい解説はそちらを参照してください。
scan系関数で解ける動的計画法っぽい問題をいくつか挙げておきます:
- AtCoder Beginner Contest 130, E – Common Subsequence
- AtCoder Beginner Contest 138, E – Strings of Impurity
- AtCoder Beginner Contest 139, C – Lower
- Educational DP Contest, F – LCS
- Educational DP Contest, T – Permutation
scanlを使った実際のコード例は、筆者によるAtCoderの問題への解答例を上げている以下のリポジトリーを参照してください。
特定の形の一次連立方程式を解く
未知数\(x_0,\ldots,x_n\)について\begin{align*}x_0&=b,\\x_0+x_1&=a_0,\\x_1+x_2&=a_1,\\x_2+x_3&=a_2,\\&\vdots\\x_{n-1}+x_n&=a_{n-1}\end{align*}という連立方程式があったとします。\(b\)と\(a_i\)は既知とします。
この方程式は、\(x_0\)がわかっているので\(x_1=a_0-x_0\), \(x_2=a_1-x_1\)という感じで順番に\(x_n=a_{n-1}-x_{n-1}\)と計算していけば解が求まります。
初期値を元に順番に計算していき、途中の値 \(x_i\) も残す……。scan系関数の出番ですね。
右辺\(a_i\)が\(\mathit{as}=[a_0,\ldots,a_{n-1}]\)というリストで与えられる場合、\(x_i\)のリスト\([x_0,x_1,\ldots,x_n]\)は scanl subtract b as により計算できます。
これはABC133-Dを解くときに遭遇したパターンです。ABC133-Dの設定では初期値\(x_0=b\)は陽には与えられておらず、何らかの方法で計算しておく必要があります。
組立除法とホーナー法
組立除法
多項式 \(f(x)=a_0+a_1x+\cdots+a_nx^n\) を \(x-b\) みたいな形の一次式で割った商と余りを求めることを考えます。もちろん汎用的な多項式除算を実装しても良いのですが、割る方の多項式が \(x-b\) という単純な形であれば、もっと効率的な方法があります。
\(f(x)\)を\(x-b\)で割った商を\(q(x)=q_0+q_1x+\cdots+q_{n-1}x^{n-1}\),余りを\(r\)とおきます。\[f(x)=q(x)(x-b)+r\]この時、両辺の係数を比較すると\begin{align*}a_0&=r-q_0b,\\a_i&=q_{i-1}-bq_i\quad(1\le i< n),\\a_n&=q_{n-1}\end{align*}という関係が成り立ちます。これを\(q\), \(r\)について解くと\begin{align*}q_{n-1}&=a_n,\\q_i&=a_{i+1}+bq_{i+1}\quad(0\le i<n-1),\\r&=a_0+bq_0\end{align*}という漸化式が得られます。この漸化式で商 \(q(x)\) と余り \(r\) を計算する方法は、組立除法と呼ばれています。高校数学で出てきたかと思います。
仮に\(q_n=0\), \(q_{-1}=r\)とおけば、\(a_i\)と\(r\)を初期値\(q_n=0\), 漸化式\(q_i=a_{i+1}+bq_{i+1}\)で計算できることになります。この漸化式は「元となるリストの要素 \(a_{i+1}\)」と「直前に計算した要素 \(q_{i+1}\)」に依存するので、scan系関数で計算できます。
具体的なコードを書いてみましょう。ここでは、多項式は昇冪の順で並べてリストにします。つまり、定数項がリストの先頭になるようにします。入力となる多項式 \(f(x)=a_0+a_1x+\cdots+a_nx^n\) はリスト \([a_0,a_1,\ldots,a_n]\) に対応させます。\(a_n\)から辿り、\(q_n=0\)が初期値なので、リストは右から辿ります。つまり、scanrを使います。
実装例は次のようになります:
kumitate :: (Num a) => [a] -> a -> ([a], a)
kumitate coeff b =
let xs = scanr (\c t -> t * b + c) 0 coeff
-- xs = [r,q_0,q_1,...,q_{n-1},0]
q = init $ tail xs -- q = [q_0,q_1,...,q_{n-1}]
r = head xs
in (q,r)
実際に試してみましょう。\(f(x)=x^2+2\) を \(x-3\) で割ることを考えます。
> kumitate [2,0,1] 3
([3,1],11)
商が \(x+3\), 余りが 11 と出てきました。\[x^2+2=(x+3)(x-3)+11\]なので正しいですね。
私が遭遇したABCの問題で、組立除法を使えるのはABC137-Fです。
ホーナー法
多項式に値を代入した時の値を計算するホーナー法の紹介をします。
多項式の値の計算の際に、展開した式 \(f(b)=a_0+a_1b+\cdots+a_nb^n\) の通りに
evalPoly :: Vector a -> a -> a
evalPoly coeff b = sum [ coeff ! i * b^i | i <- [0..n] ]
where n = length coeff + 1
と計算するのは非効率的です。\(b\)のべき乗が何回も計算されています。それよりも、\(f(b)=((\cdots(a_nb+a_{n-1})b+\cdots)b+a_1)b+a_0\) と計算した方が、足し算も掛け算もそれぞれ\(n\)回程度で済んでお得です。この計算方法をホーナー法と言います。Haskellではホーナー法は次のように foldr 一発で計算できます:
evalPoly coeff b = foldr (\c t -> t * b + c) 0 coeff
組立除法とホーナー法の関係
ここまで読んだあなたなら、そろそろ組立除法とホーナー法の関係に気付いかと思います。そう、組立除法の scanr の引数と、ホーナー法の foldr の引数は全く同じです。ホーナー法の「途中の段階の計算結果」を残すと組立除法になり、組立除法の「最終結果」だけを残すとホーナー法になるのです。
まあ、多項式 \(f(x)\) の \(x=b\) での値 \(f(b)\) は \(f(x)\) を \(x-b\) で割った余りなので、そりゃそうだろうといえばそうなのですが。
おまけ:フィボナッチ数
Haskellでフィボナッチ数のリストを定義するのに、普通は zipWith 関数を使うと思いますが、 scanl 関数も利用できます。例えば、
fibList = 0 : scanl (+) 1 fibList
あるいは
fibList = scanl (+) 0 (1 : fibList)
です。
しかし、初項である 0 と 1 がいずれの例でもバラけた位置にいるのが悲しいです。また、「直前2項の和」を「直前3項の和」みたいに変えるとscanlは使えなくなります。いやまあzipとかを組み合わせれば書けますが、それだったら最初からzipWith系を使えばいいやん…?
scan系関数の変種
オーソドックスな scanl, scanr と正格評価版の scanl', scanr' の他にも、 Data.List や Data.Vector にもいくつかバリエーションがあります。
- scanl1, scanr1
初期値を明示的に与えるfoldl, foldrに対して初期値をリストの先頭または末尾から取ってくるfoldl1, foldr1があるように、scan関数にも初期値をリストの先頭または末尾から取ってくるやつがあります。
- prescanl, prescanl’, prescanr, prescanr’ (Vector系のみ)
prescanl は scanl の後に init を適用するやつです。つまり、「最後の値」は結果のリスト(Vector)に含まれません。prescanrも同様で、「最後の値」は含まれません。
- postscanl, postscanl’, postscanr, postscanr’ (Vector系のみ)
postscanl は scanl の後に tail を適用するやつです。つまり、「初期値」が結果のリスト(Vector)から除外されます。postscanr も同様で、結果には「初期値」が含まれません。
組立除法の例は、 postscanr を使えばその後の init が不要になります。
- mapAccumL, mapAccumR
累積する値と構築されるリストに格納される値を分けられるように一般化したものと言えそうです。mapAccumL の 方は State モナドと mapM で良くね?って感じがします。
他の言語では
Haskell以外の言語にもscan系関数はあるのでしょうか。調べてみました!
- PureScript: Data.Traversable
PureScriptにもscan系関数があるようですが、Haskellのものと違って初期値を含まないようです。Haskellで言うところの postscanl / postscanr に相当する、ということでしょうか。
- Elm: List.Extra
ElmのListモジュールにはscan系関数は見当たりませんが、 list-extra パッケージに scan 系関数があるようです。
- Scala: Seq trait の scanLeft, scanRight
Scala にも Seq traint に scan系関数があります。
- Rust: std::iter::Iterator
Rustのイテレーターにもscanというメソッドがあります。ただし、状態を破壊的に更新すること、状態とイテレーターから返す型を独立させられること、scanに渡す関数がイテレーターを途中で打ち切れる(Noneを返すことでscanが返すイテレーターのnextがNoneを返す)こと、などがHaskellとの差異のようです。状態と結果の型が独立なのは、どちらかというとHaskellのmapAccum系関数に近いかもしれません。
- C++: <numeric> の std::partial_sum
C++にもscan系関数に近い関数があります。ただし、初期値は独立して与えるのではなく入力の先頭から取ってくるので、Haskellで言う所のscanl1相当です。
- OCaml, SML: なさそう?
最初に書いたように、OCamlやSMLには軽く探した感じでは見当たりませんでした。もしも見落としていたら教えていただけると幸いです。まあなかったら自分で定義すればいいだけの話なんですが。
map, filter, fold等は他の言語でも普及していますが、scan系関数も流行らせたいですね。
宣伝
技術書典7に「Haskellで戦う競技プログラミング」という本を出しました。Vectorや動的計画法も扱っています。まだ購入していないという方はBOOTHやとらのあなで購入できます。

