圏論では図式（可換図式）が多用される。図式を使うメリットは何なのか、他の表記と比べて考えてみたい。
目次
合成演算と等式による書き方
射 \(f\colon a\rightarrow b\), \(g\colon b\rightarrow c\), \(h\colon a\rightarrow b’\), \(k\colon b’\rightarrow c\) についての合成と等式を考えよう。圏の定義（合成演算）に沿った一番基本的な書き方は次のようになる：
合成：\(g\circ f\colon a\rightarrow c\), \(k\circ h\colon a\rightarrow c\)
等式：\(g\circ f=k\circ h\)
この方式のデメリットは、合成の途中で経由する対象（\(g\circ f\)の場合は\(b\), \(k\circ h\)の場合は\(b’\)）が表記に現れないことである。
合成の順番について、「先に適用する方（\(f\)や\(h\)）を先に書きたい」という意見もあるが、その場合はそういう合成記号を用意すれば良い（\(f;g\) や \(f\mathbin{\mathtt{>\!>\!>}}g\)）。その場合でも「合成の途中で経由する対象が表れない」という点は変わらない。
始域と終域を明示する書き方
「合成演算と等式による書き方」を改変し、射の名前と共に始域、終域を明示するという案が考えられる。
合成：\(\left(c\xleftarrow{g}b\right)\circ\left(b\xleftarrow{f}a\right)\), \(\left(c\xleftarrow{k}b’\right)\circ\left(b’\xleftarrow{h}a\right)\)
等式：\(\left(c\xleftarrow{g}b\right)\circ\left(b\xleftarrow{f}a\right)=\left(c\xleftarrow{k}b’\right)\circ\left(b’\xleftarrow{h}a\right)\)
煩雑である。ここまで書くのだったら図式を使うだろう。
図式による書き方
「合成演算と等式による書き方」は1次元的なものだった。図式（可換図式）は、射の合成を矢印の連鎖として、関連する複数の射を複数の連鎖からなるグラフとして（2次元的に）表現する方法である。
合成：\(a\xrightarrow{f}b\xrightarrow{g}c\), \(a\xrightarrow{h}b’\xrightarrow{k}c\), まとめると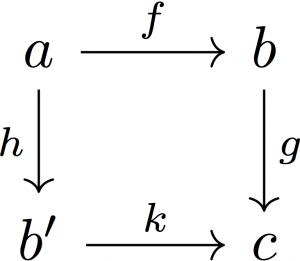
等式：が可換
図式とは、いくつかの射の合成をまとめたものであり、図式の可換性とは、それらの間の等式だと考えられる。
図式の可換性はいつでも定義されているわけではない。例えば、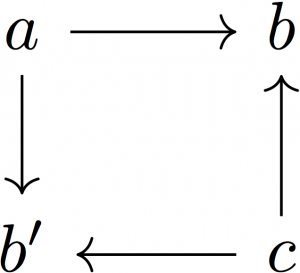
という図式には可換性は定義できない（構成する射のいずれかが同型射ならともかく）。
図式による書き方の「合成演算と等式による書き方」と比べたデメリットは、場所を取ることである。LaTeXでの書き方も煩雑（図式用のパッケージが必須）になるし、数式用のマークアップ言語MathMLは2次元的な図式を書くのに適さない。
対象が1個の圏の場合
モノイドや群は、対象が1個の圏とみなすことができる。その場合、モノイドや群の元はその圏の射である。そうすると当然、群の元に対して「合成演算と等式による書き方」の他に「図式による書き方」もできる。例えば、群 \(G\) の元 \(a\), \(g\) に対する式 \(a^{-1}ga\) は\[*\xrightarrow{a}*\xrightarrow{g}*\xrightarrow{a^{-1}}*\]と書くことができる（ただ一つの対象を\(*\)で表した）。
しかし、対象がただ一つであるということは、射の始域と終域を明示する必要性がないということである。このため、モノイドや群に関しては、図式よりも合成演算と等式による書き方の方が好まれるのだと解釈できる。
自然変換の場合（2-morphism的な書き方）
自然変換は関手圏の射と思えるので、すでに書いたような「合成演算と等式」および「図式」の書き方を利用できる。
「関手 \(F,G\colon\mathcal{C}\rightarrow\mathcal{D}\) の間の自然変換 \(\eta\colon F\rightarrow G\)」という具合である。
しかし、自然変換を「\(\eta\colon F\rightarrow G\)」だとか「\(F\xrightarrow{\eta} G\)」とか書いたのでは、関手の始域と終域（圏 \(\mathcal{C}\) や \(\mathcal{D}\)）を明示できないという問題がある。
そのため、自然変換は二重矢印を使って次のように表記されることがある：
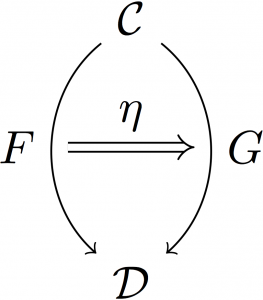この表記なら、「自然変換の始域と終域」「関手の始域と終域」の両方を書き込むことができる。このように「圏」「関手」「自然変換」の3者を明示できる書き方を「2-morphism的な書き方」と呼ぶことにしよう。
2-morphism的な書き方としては、二重矢印を使うものの他に、ストリング図 (string diagram) と呼ばれるものがある。
ストリング図については筆者はまだ勉強中なので突っ込んだことは言えないが、（可換）図式においては1枚の図式で複数通りの射の合成を表せたのに対し、1枚のストリング図は全体で1個の自然変換を表すようである。複数の自然変換の関係を表したい場合は、ストリング図の外でイコールなどを使って表現する。
二重矢印を使う表記では、圏が点、関手が辺（矢印）、自然変換が面（二重矢印）に対応した。一方、ストリング図においては、圏が面、関手が辺、自然変換が点に対応する。
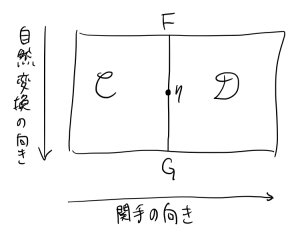
ストリング図の書き方の流儀はいくつかあるようだが、どの流儀を採用したかわかりやすいようにここでは図の外側に「自然変換の向き」と「関手の向き」を明記した。
ストリング図は、〈圏、関手、自然変換〉の他に、モノイド圏周りでも使われるようである。
自然変換の垂直合成は関手圏の射として\(F\xrightarrow{\eta}G\xrightarrow{\xi}H\)と書くこともできるが、自然変換の水平合成には2-morphism的な書き方が有利である。
まとめ
モノイドや群など、「対象が1個の圏」の射を表すときは合成演算と等式による書き方が適しているが、対象が複数ある圏の射を表すときは図式が便利である。また、自然変換のような2-morphismに対しては二重矢印やストリング図などの2-morphism的な書き方が便利である。
さらに短いまとめ
圏論では色々な表記法が使われている。かしこく使い分けよう！
