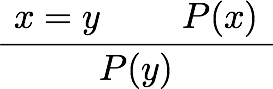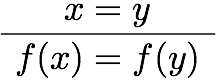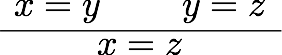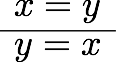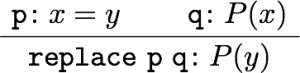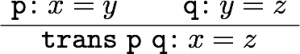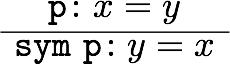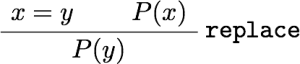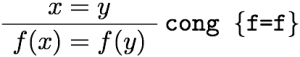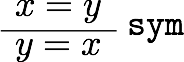「Idris」タグアーカイブ

Idrisの有界な自然数で遊んでみる(1) — 証明をつける

1件のフィードバック

前回：Idrisの有界な自然数で遊んでみる(0)

前回はIdrisで「有界な自然数の冪乗を計算する」finPower2 : Fin n -> Fin (power 2 n) という関数を実装したが、いくつか後回しにした証明があった。今回はIdrisの証明支援機能を使ってこれを埋める。

続きを読む →

Idrisの有界な自然数で遊んでみる(0)

1件のフィードバック

プログラミング言語Idris自体についての詳しい話はここではしない。このブログの昔の記事で軽く紹介したかもしれないが他人の参考になるかは分からない。

この記事を読むにあたっては、

  • ペアノ算術

は知ってないと厳しいと思われる。あとHaskell風の言語にも慣れていた方がいいか。

この記事で使うIdrisのバージョンは0.9.16である（執筆時点の最新版）。これと異なるバージョンだとコードの修正が必要かもしれない。

続きを読む →

Idrisで遊んでみた (2) — 自然数に関する命題の証明

コメントを残す

前回は等号の証明に使える公理や規則(Idrisの組み込み関数)をいくつか紹介した。

これに加え、Idrisの標準ライブラリには自然数の性質に関する補題(?)がいくつか用意されている。そのうち、後で使う2つを紹介する。

一つ目は、和と後続者に関するものである。ペアノ算術にはちょうどこのような公理があったはずだ。plusSuccRightSucc

もう一つは、和の可換性である。ペアノ算術ではこれを証明するためには帰納法を使うが、証明(関数の実装)は標準ライブラリで用意されているので、ここではそれを使うだけにとどめておく。plusCommutative

さて、前回証明したいと言っていた命題は\[x=y+\mathtt{difference}\ p\]であった。ただし、\(p\) の表す命題は \(y\le x\), Idrisの型で言うと LTE y x である。この等式を証明するには、
[sourcecode lang=”plain”]
differenceP : {x:Nat} -> {y:Nat} -> (p : LTE y x) -> (x = y + difference p)
[/sourcecode]
という型の関数を実装すれば良い。

例によって場合分けする。

  • \(y=0\), つまり p=lteZero の場合:
    • この等式は自明に成り立つ。refl を返せば良い。
  • それ以外、つまり \(x=Sx’\), \(y=Sy’\), p=lteSucc p' の場合:
    • 帰納法の仮定として differenceP p' : x' = y' + difference p' が使える。
    • この仮定を使って S x' = (S y') + difference p' を示せば良い。(difference の定義を見れば difference p = difference p' なので、S x' = (S y') + difference p は自動的に導いてくれるようだ)
    • この仮定と、先に紹介した公理、補題を使って、自然演繹っぽい証明図を書くと、prooftree1となる。
    • この証明図にIdrisの項を書き加えるとprooftree1-tとなる。ただし、一部をアンダースコアで省略している。

これらをまとめて、Idrisの式として書けば
[sourcecode lang=”plain”]
differenceP : {x:Nat} -> {y:Nat} -> (p : LTE y x) -> (x = y + difference p)
differenceP lteZero = refl
differenceP {x = S x’} {y = S y’} (lteSucc p’) = trans (trans (cong {f=S} (trans (differenceP p’) (plusCommutative _ _))) (plusSuccRightSucc _ _)) (plusCommutative _ (S y’))
[/sourcecode]
となる。一部の式をアンダースコアで省略しているが、最後の (S y') まで省略してしまうと処理系に怒られたので、そこは明示的に書いている。

今回は、自然演繹の証明図をCurry-Howard対応で翻訳することによって、命題を証明(関数を実装)した。等式の変形のところがやや煩雑になっているが、それはもとの自然演繹の証明図がそういうことになっていたことに起因するもので、Curry-Howard対応のせいでどうこうというものではない。

次回は量化子を含む命題を証明する予定である。Tacticを使った証明は筆者が不勉強なのでまだ扱わない。

Idrisで遊んでみた (1)

コメントを残す

前回はIdrisで2つの自然数を比較し、結果とその証明を返す関数 compareNats を作った。今回は、それに追加していくつかの関数を実装してみる。

まず、二つの自然数 \(x\) と \(y\) の差、\(x-y\) を計算する関数 difference を作る。\(y\le x\) の場合は良いが、\(x\lt y\) の場合はどうするか考えどころである。0を返すようにしてもよいが、ここは「\(y\le x\) であることの証拠を要求する」ことにして、\(x\lt y\) の場合は考える必要がない、という仕様にする。型を書けば
[sourcecode lang=”plain”]
difference : (x:Nat) -> (y:Nat) -> LTE y x -> Nat
[/sourcecode]
となる。前回書いたように、LTE y x は命題 \(y\le x\) に対応する型である。

実装には、例によって引数によるパターンマッチをする。

  • \(y=0\) の場合
    • \(x\) を返す。第三引数は lteZero である。
    • コードで書けば difference x 0 lteZero = x となる。
  • \(x=Sx’, \>y=Sy’\) の場合
    • 第3引数は lteSucc p の形をしている。
    • difference x' y' p によって \(x’-y’\) を計算できる。\(x-y=x’-y’\) なので、それをそのまま返せば良い。
    • コードで書けば difference (S x') (S y') (lteSucc p) = difference x' y' p となる。

まとめると
[sourcecode lang=”plain”]
difference : (x:Nat) -> (y:Nat) -> LTE y x -> Nat
difference x 0 lteZero = x
difference (S x’) (S y’) (lteSucc p) = difference x’ y’ p
[/sourcecode]
となる。

さて、よく考えてみると、第1引数 x と第2引数 y の情報は第3引数の型を見れば自動的に得られる。したがって、第1引数と第2引数は省略できるのではないか？

Idrisにはimplicit argumentsという機能があるので、この場合実際に x と y を省略できる。Implicit argumentsを使うと、difference は次のように書ける:
[sourcecode lang=”plain”]
difference : {x:Nat} -> {y:Nat} -> LTE y x -> Nat
difference {x} lteZero = x
difference (lteSucc p) = difference p
[/sourcecode]

この difference という関数は、\(y \le x\) を満たす任意の自然数 \(x\), \(y\) および \(y \le x\) の「証拠」p : LTE y x に対して、\[x = y + \mathtt{difference}\>p\]という関係を満たす。この関係式を「証明」するにはどうすればよいだろうか？

その前に、述語論理における等号の公理と、それがIdrisではどうなっているか見ておこう。自然演繹チックに書けば、述語論理の等号の公理と関連する推論規則は

  • 等号公理(反射律)equality
  • 等号規則equality2
  • 等号規則(派生)equality2b
  • 推移律equality3
  • 対称律equality4

などがある。あとの三つは最初の二つから出るので、本質的というわけではない。それぞれにIdrisの式を対応させていくと、

  • 等号公理(反射律)equality-t
  • 等号規則equality2-t
  • 等号規則(派生)equality2b-t
  • 推移律equality3-t
  • 対称律equality4-t

となる。つまり、refl, replace, cong, trans, sym という関数があって、それぞれ適切な型を持っている。

以後、命題の左に項を書いていくと上下で重複が多くなって大変なので、以後

  • 等号公理(反射律)equality-u
  • 等号規則equality2-u
  • 等号規則(派生)equality2b-u
  • 推移律equality3-u
  • 対称律equality4-u

のように、使った規則を横棒の右に書くことにする。

長くなるので、一旦記事を分割することにする。今回はここまで。

2月28日：「等号規則(派生)」を追加。

Idrisで遊んでみた (0)

依存型のあるプログラミング言語に慣れてみたいと思ってIdrisで遊んでみた。

依存型とは何かと言うと、普通の型付きラムダ計算はCurry-Howard対応によって直観主義命題論理に対応するが、依存型のあるラムダ計算は直観主義述語論理に対応する（という認識でいる）。

Curry-Howard対応によれば「型」は「命題」に対応する。そして、対応する論理は述語論理なので、「\(x=y\)」や「\(x\le 3\)」のような、項を含む命題（型）を扱うことができる。Integer型やString型をもつ値はまあ分かるが、\(x=y\) や \(x\le 3\) という型をもつ値は一体何を表しているのかと思われるかもしれない。まあ「その命題が成り立つことの証拠、あるいは証明」だと考えればいいだろう。たぶん。

なんでIdrisをやろうかと思ったかというと、文法がHaskellに似ていて取っつきやすそうだったからである。ただ、まだまだ発展途上で実用するには向かなさそうだ。まとまったリファレンスマニュアルみたいなものは見つけられなかったので、標準ライブラリの細かいところはソースコードを参照した。また、この記事のコードはVersion 0.9.11.2に向けて書いてある。

今回はIdrisで自然数(Nat 型)を扱ってみる。最初の自然数0に対応するものは Z : Nat である。ただし、型クラスがいい感じに定義されているので0と書いても良い。自然数 x の後続者(successor)は S x である。さて、さっき命題の例として \(x\le 3\) と書いたが、Idrisには LTE : Nat -> Nat -> Type というデータ構築子があって、自然数についての \(x\le 3\) という命題は LTE x 3 という型に対応する。LT : Nat -> Nat -> Type というものもあるが、これは LT x y = LTE (S x) y と定義されている。それぞれ、”Less Than or Equal to,” “Less Than” の略だと思われる。携帯電話の通信規格とは関係ない。

簡単な例として、二つの自然数を比較する関数を書いてみよう。普通の言語なら compareNats : Nat -> Nat -> Bool とでもするところだが、さっき書いたように「型は命題に対応」し、「値は証明、あるいは証拠を表す」と考えられるので、どうせなら「大きい方はどちらか、およびその証拠」を返す関数を作ってみよう。この関数の型は
[sourcecode lang=”plain”]
compareNats : (x : Nat) -> (y : Nat) -> Either (LT x y) (LTE y x)
[/sourcecode]
とする。この結果の Either (LT x y) (LTE y x) という型は、数学っぽく書けば \((x<y)\vee(y\le x)\) に相当する。

LTE x y型の値を作る（\(x\le y\) を証明する）には、2通りの関数（公理）がある。つまり、

  • lteZero : LTE Z y、つまり \(0\le y\)
  • lteSucc : LTE x y -> LTE (S x) (S y)、つまり \(x \le y \rightarrow Sx \le Sy\)

だ。compareNats の実装では x と y の値によって場合分けして、これらの関数を使って「証拠」を作ってやれば良い。

  • \(y=0\) の場合:
    • \((x<y)\vee(y\le x)\) のうち \(y \le x\) が成り立つ。LTE y x 型の値を返したいが、\(y=0\) なので lteZero が欲しい型を持つ値である。
    • したがって、Eitherのデータ構築子（\(\vee\) の導入則）と組み合わせて、Right lteZeroを返せば良い。
  • \(x=0, y=S y’\) の場合:
    • \((x<y)\vee(y\le x)\) のうち \(x<y\) が成り立つ。したがって、LT x y 型、つまり LTE (S Z) (S y') 型の値を返したい。
    • LTE Z y' 型の値であれば lteZero で得られた。これを lteSucc に食わせて lteSucc lteZero とすれば LTE (S Z) (S y') 型の値が得られる。
    • したがって、Eitherのデータ構築子（\(\vee\) の導入則）と組み合わせて、Left (lteSucc lteZero)を返せば良い。
  • \(x=Sx’,y=Sy’\) の場合:
    • まず \(x’\) と \(y’\) を比較する。比較には compareNats x' y' が使える。
    • compareNats x' y' が Left p を返してきた場合:
      • p は \(x’ < y’\) の「証拠」である。これの両辺の後続者をとれば（両辺に1加えれば）、\(Sx'<Sy’\) の「証拠」、つまり \(x<y\) の「証拠」になる。
      • つまり lteSucc p が \(x<y\) の「証拠」である。\((x<y)\vee(y\le x)\) のうち成り立つのは \(x<y\) の方なので、Left (lteSucc p) を返せば良い。
    • compareNats x' y' が Right q を返してきた場合:
      • q は \(y’ \le x’\) の「証拠」である。これの両辺の後続者をとれば（両辺に1加えれば）、\(Sy’\le Sx’\) の「証拠」、つまり \(y\le x\) の「証拠」になる。
      • つまり lteSucc q が \(y\le x\) の「証拠」である。\((x<y)\vee(y\le x)\) のうち成り立つのは \(y\le x\) の方なので、Right (lteSucc q) を返せば良い。

以上をまとめると次のようなコードになる:
[sourcecode lang=”plain”]
compareNats : (x : Nat) -> (y : Nat) -> Either (LT x y) (LTE y x)
compareNats x Z = Right lteZero
compareNats Z (S y’) = Left (lteSucc lteZero)
compareNats (S x’) (S y’) = case compareNats x’ y’ of
Left p => Left (lteSucc p)
Right q => Right (lteSucc q)
[/sourcecode]
あるいは、either : (a -> c) -> (b -> c) -> (Either a b) -> c 関数を使えば次のようにも書ける:
[sourcecode lang=”plain”]
compareNats : (x : Nat) -> (y : Nat) -> Either (LT x y) (LTE y x)
compareNats x Z = Right lteZero
compareNats Z (S y’) = Left (lteSucc lteZero)
compareNats (S x’) (S y’) = either (Left . lteSucc) (Right . lteSucc) (compareNats x’ y’)
[/sourcecode]

今回はここまで。

なお、今回の記事では

  • Curry-Howard対応
  • Haskell（またはそれに類した言語）
  • ペアノ算術

あたりの知識を仮定した。初心者向けではなく、自分のための備忘録的な感じで書いた。