この記事は 数学とコンピュータ Advent Calendar 2017 の14日目の記事です。
以前このブログでも告知しましたが、2ヶ月前から、「週刊 代数的実数を作る」と題して、代数的数の計算機上での実装について Web 上で連載しています:
この記事では、「週刊 代数的実数を作る」でこれまで扱ったトピックを振り返り、これからの方向性を述べます。この記事を読む前に連載に目を通している必要はなく、この記事で概要を把握してから連載の方を読むのでも構いません。
(本当は代数的数の実装を利用して有理関数の部分分数分解と不定積分でもやってやろうと思っていたのですが、現状の実装が遅すぎるので断念しました。)
目次
連載について
「週刊 代数的実数を作る」の記念すべき最初の記事(#0 と #1)を公開(創刊)したのが、ちょうど2ヶ月前(10月14日)であり、12月14日の時点では #7 まで公開しています。
ブログの創刊告知では「果たしていつまで続くかは不明である。」と書いていますが、(休載を挟みつつも)なんとか2ヶ月間続けられました。
現在予定している記事の本数は全部で15か16程度なので、おおよそ折り返し地点に差し掛かっていると言って良いでしょう(予定している内容の分割を増やすかもしれないので、記事の本数はもっと増えるかもしれません)。
遊んでみよう
#7 までの実装例は
https://github.com/minoki/algebraic-real-article/tree/impl
に置きました(記事の方とリポジトリを共有するのが賢いかはわかりませんが)。
取ってくるには
$ git clone --branch impl --single-branch https://github.com/minoki/algebraic-real-article.git algebraic-real
という感じにブランチ (impl) を指定します。
Haskell Stack をインストール済みの方は、
$ cd algebraic-real/ $ stack repl
ですぐに試すことができます(Stack をまだインストールしていないという方は、頑張ってください。つい最近、 Haskell の環境構築が大変だという話題がありましたね)。
REPL のプロンプトが長すぎると思ったら :set prompt "> " でも実行すれば良いでしょう(以下の実行例ではプロンプトを単に > で示します)。
現在の実装では多項式の不定元は ind ですが、より馴染み深い x を使えるようにしておきます:
> let x = ind
では、 #7 までの実装でどういうことができるようになり、どういうことがまだできないのか見てみましょう。
ステップ1:整数係数多項式の根の列挙
整数係数多項式の実根をリストとして列挙するには、 realRoots関数を使います。重複度は考慮されません。
> :t realRoots realRoots :: UniPoly Integer -> [AlgReal]
例として、 \(x^3-4x^2+4x-1\) の根を列挙してみましょう。
> realRoots (x^3 - 4*x^2 + 4*x - 1) [AlgReal (UniPoly [-1,4,-4,1]) 1 (5 % 16) (5 % 8),AlgReal (UniPoly [-1,4,-4,1]) (-1) (5 % 8) (5 % 4),AlgReal (UniPoly [-1,4,-4,1]) 1 (5 % 2) (5 % 1)]
なにやら長々と表示されましたが、よく見ると3個の値からなるリストであることがわかります。つまり、その3個の値が \(x^3-4x^2+4x-1=0\) の実根です。小さい方から順に
AlgReal (UniPoly [-1,4,-4,1]) 1 (5 % 16) (5 % 8)AlgReal (UniPoly [-1,4,-4,1]) (-1) (5 % 8) (5 % 4)AlgReal (UniPoly [-1,4,-4,1]) 1 (5 % 2) (5 % 1)
と表示されています。それぞれ \(\alpha_1,\alpha_2,\alpha_3\) と呼ぶことにします。
ここで、 \(\alpha_1\)、つまり AlgReal (UniPoly [-1,4,-4,1]) 1 (5 % 16) (5 % 8) をより詳しく見ていきましょう。AlgReal はデータ構築子の名前です。
- 最初の
UniPoly [-1,4,-4,1]は、この数 \(\alpha_1\) を根としてもつ多項式、 \(x^3-4x^2+4x-1\) を表します。係数のリストを降べきの順で表しています。 - 次の
1は、 \(x^3-4x^2+4x-1\) の \(\alpha_1\) における符号の変化を表します。ここでは負から正に変わるので1ですが、正から負に変わる場合は-1となります(\(\alpha_2\) はそうなっています)。 - 後ろ2つ
5 % 16と5 % 8は \(\alpha_1\) を含む有理数の区間です。多項式は一般に複数の根を持つので、そのうちのどれを表したいのかを区間を使って指定します。Haskellでの有理数の表記は分子と分母を区切るのに%を使うため、これは、 \(\frac{5}{16}<\alpha_1<\frac{5}{8}\) を意味します。
\(\alpha_2\) と \(\alpha_3\) も同様で、\(\frac{5}{8}<\alpha_2<\frac{5}{4}\), \(\frac{5}{2}<\alpha_3<5\) という関係が成り立ちます。
以降の REPL でこれら \(\alpha_1,\alpha_2,\alpha_3\) を参照できるように、名前をつけておきます:
> let [a1,a2,a3] = realRoots (x^3 - 4*x^2 + 4*x - 1)
(または let [a1,a2,a3] = it でも良い)
根の近似値を計算してみましょう。(本当は #5 あたりで代数的実数を浮動小数点数に変換する関数を実装しておけばよかったのですが、執筆当時はそこまで手が回りませんでした)
\(\alpha_1\) の近似値は、次の式を評価するとわかります:
> let approx x = case intervals x !! 100 of Iv a b -> (fromRational a, fromRational b) > approx a1 (0.38196601125010515,0.38196601125010515)
\(\alpha_2\) と \(\alpha_3\) についても同様に計算してみます:
> approx a2 (1.0,1.0) > approx a3 (2.618033988749895,2.618033988749895)
ステップ2:代数的実数どうしの比較演算
代数的実数と有理数、または代数的実数どうしの大小、等号を比較できます。
> 1 < a1 False > a1 < a3 True > a1 == 0.38196601125010515 False > a1 > 0.38196601125010515 True > a3 == 2.618033988749895 False > a3 < 2.618033988749895 True
賢い読者諸君は \(x^3-4x^2+4x-1=0\) の根の1つが 1 であること、すなわち \(\alpha_2\) が整数 1 に等しいことに気づいたかもしれません。連載で実装したプログラムでもそのことが確かめられます:
> a2 == 1 True
しかし、先ほど見たように、 \(\alpha_2\) の表示は 1 とは異なりました。このように、現在の実装では、代数的実数の表示は一意的ではありません。しかし、代数的実数の比較は、正確に行うことができます。
代数的実数の表示(の多項式の部分)を一意的にしたい、有理数を有理数っぽく表示したい、という場合には、多項式の因数分解を行う必要があります。これは今後の連載で取り扱う予定です(後述)。
ステップ3:代数的実数どうしの四則演算
四則演算もできます。
> a1 + 1 AlgReal (UniPoly [-10,15,-7,1]) 1 (21 % 16) (13 % 8) > approx (a1 + 1) (1.381966011250105,1.381966011250105) > a1 * 2 AlgReal (UniPoly [-8,16,-8,1]) 1 (5 % 8) (5 % 4) > approx (a1 * 2) (0.7639320225002103,0.7639320225002103) > a1^2 AlgReal (UniPoly [1,-11,33,-33,11,-1]) (-1) (25 % 256) (225 % 1024) > approx (a1^2) (0.14589803375031546,0.14589803375031546)
根と係数の関係はご存知だと思います。 \(\alpha_1,\alpha_2,\alpha_3\) が \(x^3-4x^2+4x-1\) の根なので、 \begin{align*}\alpha_1+\alpha_2+\alpha_3&=4,\\\alpha_1\alpha_2+\alpha_2\alpha_3+\alpha_3\alpha_1&=4,\\\alpha_1\alpha_2\alpha_3&=1\end{align*}が成り立つはずです。確かめてみましょう。
> a1 + a2 + a3 == 4 True > a1 * a2 + a2 * a3 + a3 * a1 == 4 True > a1 * a2 * a3 == 1 True
a1 + a2 + a3 と a1 * a2 * a3 は割とすぐに答えが返ってきますが、 a1 * a2 + a2 * a3 + a3 * a1 は少し時間がかかったと思います。これも、多項式の次数が不必要に増大しているのが原因です。
本来、 a1 * a2 + a2 * a3 + a3 * a1 の計算結果は整数 4 なので、この数は \(x-4\) という1次の多項式の根として表すことができるはずです。しかし実際には
> a1 * a2 + a2 * a3 + a3 * a1 AlgReal (UniPoly [141870605563289062918656,-1811266186759862482647360,10711240522009097990857344,-39215503407943837570924152,100181836212328458393605613,-190748978459199318649832307,282256318717360189440143499,-334093556159001268286573125,323050926287069207967141182,-259277233739394812614924306,174869950952335917115807068,-100083692506183732993933220,48988316597418489089227473,-20635368460431757509735159,7517663809544307423860361,-2377953685020112520219583,655046090904821520483843,-157480600253400304780581,33088292367077230891047,-6079933856024881689969,976937829888192296157,-137156392092628670091,16797011221526048073,-1789826895907403727,165349436768673795,-13180352737195509,900853299206883,-52363452427869,2560972966596,-103906245300,3431083194,-89772254,1788985,-25487,231,-1]) (-1) (15425 % 4096) (4525 % 1024) > degree (definingPolynomial it) Just 35
と、35次の多項式の根として表されてしまっています。これでは計算に時間がかかるのも無理はありません。やはり多項式の因数分解が必要です。
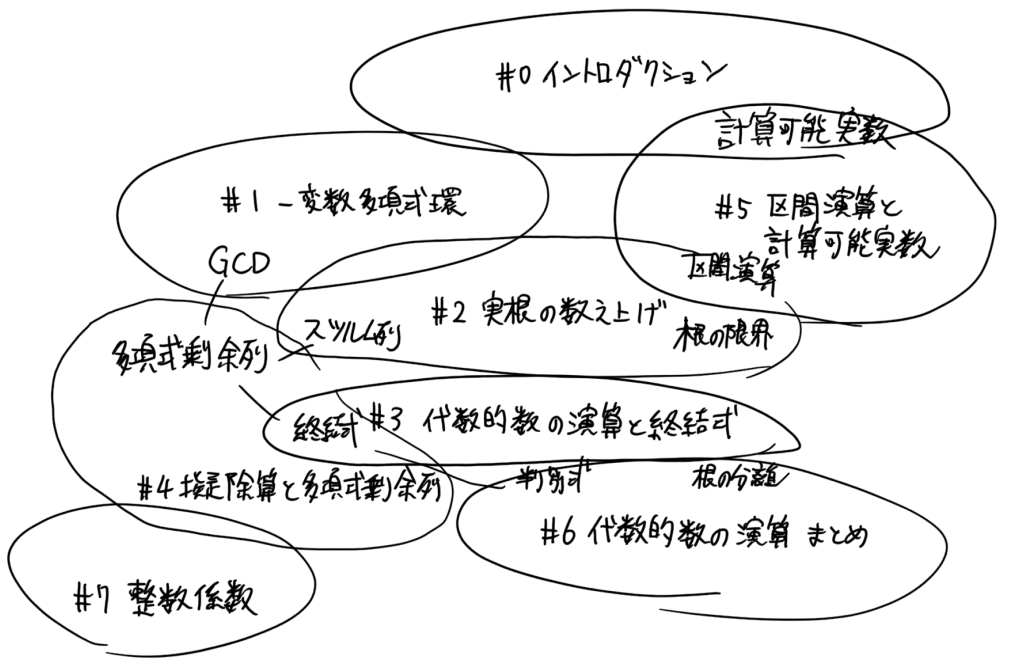
週刊 代数的実数を作る #7.5 総集編
ここに至るまでの道のりを振り返ってみましょう。
#0 イントロダクション
2017年10月14日 / キーワード:計算可能実数
計算機上で扱える実数について語りました。
計算可能実数は、我々が思いつくほぼ全ての実数を表現できますが、表現力が高すぎて、比較演算が停止しないという難点があります。
そこで、比較演算が必ず停止するように、考える実数の範囲(実数のクラス)を狭めることを考えます。比較演算が停止するクラスとして、代数的実数があります。
この回では代数的実数の表し方、実装の方針について、ざっくりと述べました。
#1 一変数多項式環
2017年10月14日 / キーワード:一変数多項式環, ホーナー法, ユークリッドの互除法, 係数膨張
多項式を表す型を用意し、多項式除算、ユークリッドの互除法など、多項式に関する基本的なアルゴリズムを実装しました。
この際、互除法を素朴に実装すると係数膨張という現象が起こることを見ました。
#2 実根の数え上げ
2017年10月21日 / キーワード:スツルムの定理, 根の限界
スツルムの定理によって、多項式の実根の個数を正確に数え上げることができることを見ました。
代数的実数を表す型を用意し、有理数係数多項式の実根を列挙する関数を実装しました。
#3 代数的数の演算と終結式
2017年10月28日 / キーワード:終結式, シルベスター行列
代数的数どうしの演算をどのように実装するかについて述べました。その際に終結式という演算を使いました。
終結式はユークリッドの互除法と同様のアルゴリズムで計算できますが、多項式を係数とする多項式についての互除法は、係数が体でないので一筋縄にいかないという問題に直面しました。
#4 擬除算と多項式剰余列
2017年11月5日 / キーワード:擬除算, 多項式剰余列, 部分終結式
多項式除算およびユークリッドの互除法は係数が体(有理数や有理関数)でないと使えませんが、それを一般化(係数が整数や多項式の場合も含む)したものとして、擬除算と多項式剰余列を扱いました。
#5 区間演算と計算可能実数
2017年11月18日 / キーワード:区間演算, 浮動小数点数, IEEE754, 計算可能実数
実数の区間演算を扱い、計算可能実数を表す型を簡易的に実装しました。
#6 代数的数の演算 まとめ
2017年11月25日 / キーワード:判別式, 根の分離
終結式の特別な場合である判別式を扱い、それを根の距離の評価(根の分離)に利用できることを見ました。
その後、 #3 からのまとめとして、終結式と区間演算を組み合わせて、代数的実数についての四則演算を一通り実装しました。
#7 整数係数
2017年12月10日 / キーワード:可換環, 整域
これまでに代数的数の定義多項式を有理数係数多項式としていましたが、今後のことを考え、整数係数多項式に切り替えます。
GCD のアルゴリズムは、 #4 で扱った多項式剰余列のアルゴリズムを利用すれば、整数係数や多項式係数(係数が整域)でも問題なく実装できます。
整数係数や多項式係数で同じ関数を使い回せるように、Haskellの型クラスを使って、整域や GCD 整域を表すことにしました。
次回予告(今後の予定)
多項式の因数分解
現状の実装では、代数的実数を表す多項式の次数が不必要に増大します。それを改善するためには、多項式を因数分解しなくてはなりません。
整数係数多項式を因数分解する古典的な方法として Kronecker の方法がありますが、この方法は言わば総当たりであり、非常に遅いです。
多項式を因数分解するための現代的な方法は有限体を利用するものなので、この連載でもそれを取り上げます。
多くの読者にとって有限体は馴染みのないものだと思われるので、有限体についてはなるべく基礎から説明するように心がけます。(すでに数学科以外には厳しい連載となっているかもしれませんが……)
「多項式の因数分解」編は、全部で5〜6回の分量を見込んでいます。
(連載の最初の方に「高速化は後回しにしてなるべく素朴な方法で」と書いた気もしますが、これに反して「因数分解の高速化」に取り組むことになります。理論の単純さを優先させた非実用的なアルゴリズムのままでは、「実例で遊ぶ」ことが困難になってしまうので、ある種のトレードオフです。)
実閉体
代数的実数についての演算は #6 で一通り実装しました。…というわけでもなくて、「代数的実数を係数とする多項式の実根を求める操作」がまだ実装されていません(特殊な場合である「代数的実数の \(n\) 乗根」はすでに実装しましたが)。
これも、終結式を繰り返し使っていけば「整数係数多項式の実根を求める操作」に帰着できます。例で説明すると、
\[x^2-2\sqrt{3}x+1\]
の根は
\[(x^2-2\sqrt{3}x+1)(x^2+2\sqrt{3}x+1)\]
の根でもあり、後者は
\[(x^2-2\sqrt{3}x+1)(x^2+2\sqrt{3}x+1)=x^4-10x^2+1\]
と整数係数になります。整数係数多項式の実根の列挙はすでに実装しているので、その中から元の多項式の根を選び出してやれば良いのです。多項式 \(x^2-2\sqrt{3}x+1\) から多項式 \(x^4-10x^2+1\) を得るのに終結式が利用できます。
「代数的実数を係数とする多項式の実根を求める操作」を実装すると、代数閉体 \(\overline{\mathbf{Q}}\) (\(\overline{\mathbf{Q}}\) 係数の多項式の根が全て \(\overline{\mathbf{Q}}\) の元)まであと一歩という感じがします。実際、そういう性質を持った体は実閉体と呼ばれ、代数的実数は実閉体の一つの例となります。
複素数と代数閉体
これまでは実数の範囲の代数的数を扱ってきましたが、複素数に範囲を広げます。これにより、 \(\sqrt{-1}\) や \(\frac{-1+\sqrt{-3}}{2}\) のような複素数をはじめとして、任意の整数係数多項式の根を扱うことができるようになります。
これはまた、我々が計算機上で正確に扱える代数閉体を手に入れることを意味します。
発展的な話題
定期的な連載としては「代数閉体」で終わりになると思いますが、気が向いたら関連する話題や応用例について書くかもしれません。
現状、「関連する話題」または「応用例」として考えているものをいくつか挙げておきます:
- 連分数
- 有理関数の部分分数分解と不定積分
- 作図可能な数
- 超越拡大(\(\overline{\mathbf{Q}}(\pi)\) など)
- さらなる実装の効率化
最後に
そういえば、連載の方 (https://miz-ar.info/math/algebraic-real/) にはコメント欄がついていません。コメントしたい方は代わりにこっちのブログ記事にコメントするとか、はてブを使うとか、ツイッターでURLつきでつぶやくとかしてください。
今年の Advent Calendar が終わっても「週刊 代数的実数を作る」は終わりません。これからも「週刊 代数的実数を作る」をよろしくお願いします。

ピンバック: 重力プログラミング入門「第2回:重力波を解析する」 | IT技術情報局
今晩は.
> ステップ3:代数的実数どうしの四則演算
私の環境で実行すると,例えば,次のような不具合が現れます.
> (a1 – 1) + (1 – a1)
AlgReal (UniPoly [-120,400,-504,311,-100,16,-1]) (-1) ((-5) % 16) ((-5) % 32)
ご指摘ありがとうございます。おっしゃる通りのバグを確認したので、修正しました。git pull して再度お試しください。
修正,確認しました.因数分解の実装後にしようかとも思いましたが,忘れそうなのでここでお尋ね致します.現在のコードでは代数的数の演算毎に根の分離を実行しておられますが,これは余りにハイコストですね.因数分解による既約因子の抽出以外に,何か改善策をお持ちでしょうか?
返信が遅くなってしまってすみません。現在の感触では、ボトルネックは根の分離や因数分解ではなく、終結式の計算にあると睨んでいます。高速化に関しては、なるべくプロファイルを取って定量的にやっていきたいと思います。
連載,お疲れ様です.#14の
> 単に分離区間の両端で符号が異なっていることを確かめれば良い
で済ませる為には,例えば,x^2+2*sqrt(2)*x+2->x+sqrt(2) のような,代数体上の多項式の無平方化が必要かと思います.
コード上ではすでに無平方分解を行なっています (yun 関数)。まあ、本文の方でも無平方性に関して一言あった方がいいかもしれません。
ピンバック: 技術書典5に代数的数を作る本を出します | 雑記帳