OpenGL での 3DCG で使われる投影行列について、自分用にメモっておく。
情報源:
- https://www.khronos.org/opengl/
- https://www.khronos.org/registry/OpenGL/index_gl.php
- OpenGL Core Profile, Compatibility Profile, GLU など
- OpenGL 2.1 Reference Pages
- https://www.khronos.org/registry/OpenGL/index_gl.php
- GLM (OpenGL Mathematics)
座標
ベクトル \(v\) は
\[v=\begin{pmatrix}x\\y\\z\\w\end{pmatrix}\]
の4成分のベクトルで表される。
おなじみの3次元のベクトルに変換するには、\(x,y,z\) を \(w\) で割る:
\[\begin{pmatrix}x/w\\y/w\\z/w\end{pmatrix}\in\mathbf{R}^3\]
\(w=0\) の場合は、無限遠点に対応する。
行列の成分
行列の成分をメモリに格納する順番を確認しておく。行列を OpenGL の関数(UniformMatrix など)と受け渡しする際に重要になる。
デフォルト (transpose=false) では、 column-major である。
\[\begin{pmatrix}
\mathrm{a[0]} & \mathrm{a[4]} & \mathrm{a[8]} & \mathrm{a[12]} \\
\mathrm{a[1]} & \mathrm{a[5]} & \mathrm{a[9]} & \mathrm{a[13]} \\
\mathrm{a[2]} & \mathrm{a[6]} & \mathrm{a[10]} & \mathrm{a[14]} \\
\mathrm{a[3]} & \mathrm{a[7]} & \mathrm{a[11]} & \mathrm{a[15]}
\end{pmatrix}\]
transpose を true とした場合は、 row-major となる。
これに合わせる形で、 GLSL や GLM の mat4 型の成分は次のような順番になる:
\[\begin{pmatrix}
\mathrm{a[0][0]} & \mathrm{a[1][0]} & \mathrm{a[2][0]} & \mathrm{a[3][0]} \\
\mathrm{a[0][1]} & \mathrm{a[1][1]} & \mathrm{a[2][1]} & \mathrm{a[3][1]} \\
\mathrm{a[0][2]} & \mathrm{a[1][2]} & \mathrm{a[2][2]} & \mathrm{a[3][2]} \\
\mathrm{a[0][3]} & \mathrm{a[1][3]} & \mathrm{a[2][3]} & \mathrm{a[3][3]}
\end{pmatrix}\]
数学の表記で言う \(a_{ij}\) が a[j][i] と、 \(i\) と \(j\) の順番が入れ替わるので注意されたい。
正射影
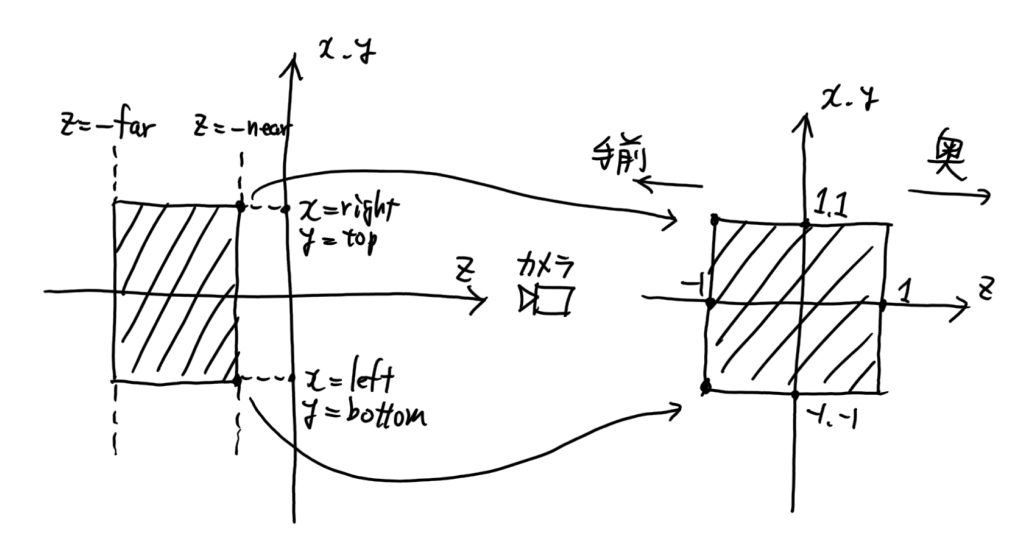
セッティング:
右手系 vs 左手系を考えるのが面倒なので、x, y 軸はまとめて描いた。
左の網掛け部分が右の網掛け部分(立方体)に移る。
関数:
- GLM: glm::ortho(left, right, bottom, top, near, far) (
<glm/gtc/matrix_transform.hpp>, API docs の該当ページ) - 古い OpenGL: glOrtho(left, right, bottom, top, near, far) (OpenGL 2.1 Reference Pages の該当ページ)
行列表示:
\[\begin{pmatrix}
\frac{2}{\mathrm{right}-\mathrm{left}} & 0 & 0 & -\frac{\mathrm{right}+\mathrm{left}}{\mathrm{right}-\mathrm{left}} \\
0 & \frac{2}{\mathrm{top}-\mathrm{bottom}} & 0 & -\frac{\mathrm{top}+\mathrm{bottom}}{\mathrm{top}-\mathrm{bottom}} \\
0 & 0 & -\frac{2}{\mathrm{far}-\mathrm{near}} & -\frac{\mathrm{far}+\mathrm{near}}{\mathrm{far}-\mathrm{near}} \\
0 & 0 & 0 & 1
\end{pmatrix}\]
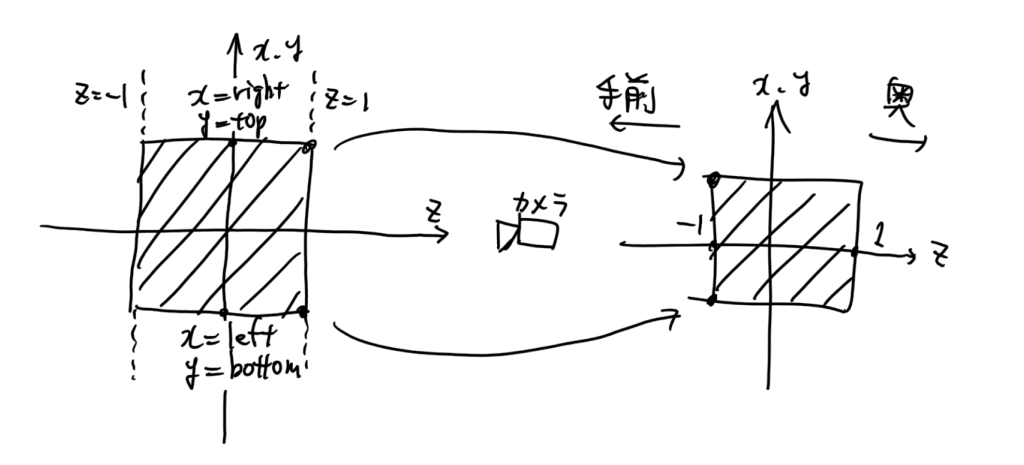
平面 z=0 を対象とする場合
セッティング:
平面 z=0 上のものを写したいという場合。
一般の場合の正射影で near = -1, far = 1 とした場合に相当する。
関数:
- GLM: glm::ortho(left, right, bottom, top) (
<glm/gtc/matrix_transform.hpp>, API docs の該当ページ)- glm::ortho(left, right, bottom, top, -1, 1) と等価
- GLU: gluOrtho2D(left, right, bottom, top) (OpenGL 2.1 Reference Pages の該当ページ)
行列表示:
\[\begin{pmatrix}
\frac{2}{\mathrm{right}-\mathrm{left}} & 0 & 0 & -\frac{\mathrm{right}+\mathrm{left}}{\mathrm{right}-\mathrm{left}} \\
0 & \frac{2}{\mathrm{top}-\mathrm{bottom}} & 0 & -\frac{\mathrm{top}+\mathrm{bottom}}{\mathrm{top}-\mathrm{bottom}} \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}\]
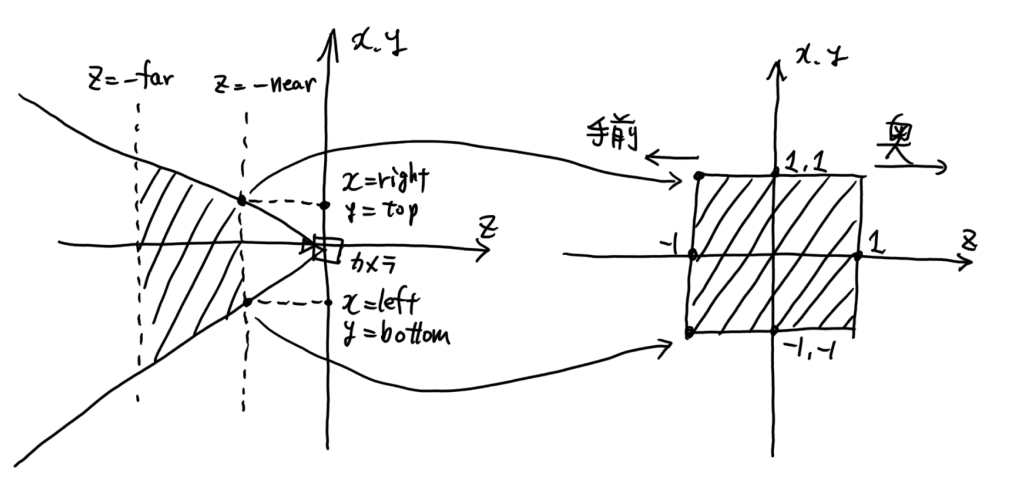
四角錐(遠近法)
セッティング:
カメラは原点にある。
関数:
- GLM: glm::frustum(left, right, bottom, top, near, far) (
<glm/gtc/matrix_transform.hpp>, API docs の該当ページ) - 古い OpenGL: glFrustum(left, right, bottom, top, near, far) (OpenGL 2.1 Reference Pages の該当ページ)
行列表示:
\[\begin{pmatrix}
\frac{2\mathrm{near}}{\mathrm{right}-\mathrm{left}} & 0 & \frac{\mathrm{right}+\mathrm{left}}{\mathrm{right}-\mathrm{left}} & 0 \\
0 & \frac{2\mathrm{near}}{\mathrm{top}-\mathrm{bottom}} & \frac{\mathrm{top}+\mathrm{bottom}}{\mathrm{top}-\mathrm{bottom}} & 0 \\
0 & 0 & -\frac{\mathrm{far}+\mathrm{near}}{\mathrm{far}-\mathrm{near}} & -\frac{2\mathrm{far}\cdot\mathrm{near}}{\mathrm{far}-\mathrm{near}} \\
0 & 0 & -1 & 0
\end{pmatrix}\]
正射影の場合は \(\mathbf{R}^3\) の等長変換として見做すことができたが、こちらはそうではない。具体的には、 z 方向の間隔が保たれない。
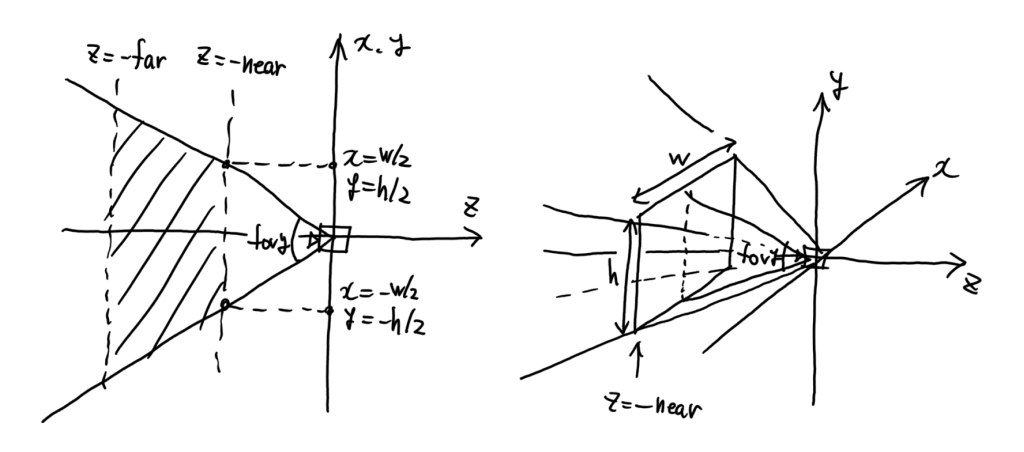
遠近法
(右手系の場合)
z 軸(の負の部分)を中心とする。カメラから見た時の、幅 / 高さ つまりアスペクト比を aspect 、高さ方向の視野角を fovy (fov: field of view angle) として指定する。
図中の w, h は \(h/2=\mathrm{near}\cdot\tan(\mathrm{fovy}/2), w=\mathrm{aspect}\cdot h\) で定める。
関数:
- GLM: glm::perspective(fovy, aspect, near, far) (
<glm/gtc/matrix_transform.hpp>, API docs の該当ページ)- glm::frustum(-w/2, w/2, -h/2, h/2, near, far) と等価
- 角度 fovy の単位は、ラジアンである。
- GLU: gluPerspective(fovy, aspect, near, far) (OpenGL 2.1 Reference Pages の該当ページ)
- 角度 fovy の単位は、度である。
行列表示:
\[\begin{pmatrix}
\frac{1}{\mathrm{aspect}\cdot\tan(\mathrm{fovy}/2)} & 0 & 0 & 0 \\
0 & \frac{1}{\tan(\mathrm{fovy}/2)} & 0 & 0 \\
0 & 0 & -\frac{\mathrm{far}+\mathrm{near}}{\mathrm{far}-\mathrm{near}} & -\frac{2\mathrm{far}\cdot\mathrm{near}}{\mathrm{far}-\mathrm{near}} \\
0 & 0 & -1 & 0
\end{pmatrix}\]

ピンバック: GLMのマニュアルがヘボいので自分で書き始めた | 雑記帳