浮動小数点数の文字列化（基数変換）

動機付けと問題

計算機の内部では二進浮動小数点数が使われることが多い一方で、プログラムのソースコードやテキストベースのデータ形式（例：JSON）では十進小数が使われることが多い。

データのシリアライズ等で、内部的な二進浮動小数点数を十進小数に変換して、再度二進小数に戻すという操作が考えられる。この時、元々の二進小数の値が保持されることが望ましい。

有限桁の二進小数は原理的には有限桁の十進小数で表現できるが、指数部が大きかったり小さかったりすると仮数部の桁数も膨張するため実用的ではない。

そこで、基数変換の際に丸めが発生することを許容して、二進小数→十進小数→二進小数の変換が恒等写像となるようにしたい。ただし丸めの方法は最近接丸めであるとする。この時、

  • 途中の十進小数の仮数部は何桁あれば十分か？
  • なるべく短い桁数の十進小数を、正しい丸めで得るためのアルゴリズムはどのようなものか？

という問題が考えられる。

目次

桁数の問題（round tripする桁数）

桁数の問題は、Matulaの論文（1968）で解決されている：

\(\beta\)進\(n\)桁の浮動小数点数を\(\nu\)進\(m\)桁の浮動小数点数（いずれも指数部の範囲に制限は設けない）を経由して元の形式に戻す時に元の値と同一の値が得られる必要十分条件は、\(\nu^{m-1}>\beta^n\)である。ただし、\(\beta\ge 2\), \(\nu\ge 2\), \(n\ge 1\), \(m\ge 1\)で、\(\beta\)と\(\nu\)はいかなる\(i,j>0\)についても\(\beta^i\ne\nu^j\)であるとする。

この不等式を\(m\)について解くと\[m>1+n\log_\nu \beta\]となり、\(n\)について解くと\[(m-1)\log_\beta\nu>n\]となる。C言語の DECIMAL_DIG や {FLT,DBL,LDBL}_DIG の規定にはこの辺の不等式が利用されている。

動機付けに書いた二進→十進→二進の場合は\(\beta=2\), \(\nu=10\)である。倍精度（\(n=53\)）を十進に変換して元に戻るためには十進での桁数\(m\)が17以上であることが必要十分である（\(10^{15}<2^{53}<10^{16}\)なので）。

リンク：

基数変換（文字列化）のアルゴリズム

二進浮動小数点数を

  • （round tripするという意味で）情報の喪失が起きない範囲で
  • なるべく短い桁数で
  • 正しい丸めで

十進小数に変換したい。要は文字列化である。

KnuthのTAoCP Vol. 2の演習問題4.4.3によると、Dragon4よりも前にD. Tarantoによる仕事があるらしいが、ここでは省略する。

Dragon4（1990年）

この分野では古典的なアルゴリズムっぽい。多倍長整数を使うらしい。

  • Guy L. Steele and Jon L. White. 1990. How to print floating-point numbers accurately. SIGPLAN Not. 25, 6 (Jun. 1990), 112–126. DOI:https://doi.org/10.1145/93548.93559
  • Guy L. Steele and Jon L. White. 1990. How to print floating-point numbers accurately. In Proceedings of the ACM SIGPLAN 1990 conference on Programming language design and implementation (PLDI ’90). Association for Computing Machinery, New York, NY, USA, 112–126. DOI:https://doi.org/10.1145/93542.93559
    • ACMから無料でPDFをダウンロードできる。

論文としての発表は1990年だが、アルゴリズム自体は1970年代から1980年代にかけて構築・改良されていったらしい。

Dragon4の改良版もあるらしいが、多倍長整数を使うという点ではDragon4と変わらないためここでは割愛。

Grisu3（2010年）

固定長整数だけを使って二進十進変換を行う3つのアルゴリズムを提示する。

  1. 基本的なアルゴリズム（Grisu）
  2. より短い（しばしば最短な）十進表示を得るアルゴリズム（Grisu2）
  3. 最短の十進表示を得る、失敗しうるアルゴリズム（Grisu3）

最後のGrisu3が（失敗した場合は他のアルゴリズムを併用するという形で）よく利用されるようだ。

Grisuという名前の由来はドラゴンが登場するイタリアのTVアニメらしい。

Ryū（2018年）

固定長整数だけを使うアルゴリズムで、Grisu3と比べても高速であることを主張している。ルックアップテーブルを使う。

  • Ulf Adams. 2018. Ryū: fast float-to-string conversion. In Proceedings of the 39th ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI 2018). Association for Computing Machinery, New York, NY, USA, 270–282. DOI:https://doi.org/10.1145/3192366.3192369
  • Ulf Adams. 2018. Ryū: fast float-to-string conversion. SIGPLAN Not. 53, 4 (April 2018), 270–282. DOI:https://doi.org/10.1145/3296979.3192369
    • オープンアクセス。

Dragon4を詳しく見る

筆者の使用場面（LunarML）での要件は

  • 速度は気にしない
  • 多倍長整数を使える
  • アルゴリズムが単純な方が望ましい

である。この条件ではDragon4が良さそうだと思った。正確にはDragon4は「固定桁出力」にも対応して複雑になっているので、ここで解説するアルゴリズムはDragon4ではなく同論文中のFixed-Precision Positive Floating-Point Printout ((FPP)²)である。

アルゴリズム(FPP)²の入出力は次のようになる：

  • 入力：
    • \(b\)進\(p\)桁の正の浮動小数点数\(v=f\times b^{e-p}\), ただし\(f\)は\(0<f<b^p\)を満たす整数（仮数部）
    • 出力の基数\(B\)
  • 出力：
    • 整数\(H\)（出力の指数部を表す）、整数\(N\)
    • \(B\)進表示での仮数部\(D_k\) (\(N\le k\le H\))
  • 出力の満たす条件：
    • （\(V:=\sum_{i=N}^H D_i\times B^i\)とおく）
    • \(\frac{v^-+v}{2}<V<\frac{v+v^+}{2}\)（出力を最近接丸めで元の形式に戻した時に元の値に戻る）
    • \(H\)は最小で、\(N\)は最大
    • \(\lvert V-v\rvert\le \frac{B^N}{2}\)（最近接丸めである）

ただし、\(v^+\)と\(v^-\)はそれぞれ\(v\)の後続者 (successor)、前任者 (predecessor) である。つまり、「ひとつ隣の浮動小数点数」である。

元の論文ではIEEE 754に定められた非正規化数を考慮していない。非正規化数の場合は\(e=\mathit{emin}+1\), \(0<f<b^{p-1}\)とすれば良いだろう。

アルゴリズム(FPP)²は「準備パート」と「出力パート」からなる。

準備パート（論文のSimple-Fixupに相当）：

  • 入力：
    • 整数\(b\), \(p\), \(f\), \(e\), \(B\)
  • 出力：
    • 整数\(k\), \(S\), \(R\), \(M^+\), \(M^-\)
    • 以下を満たす：
      • \(k=1+\left\lfloor\log_B\frac{v+v^+}{2}\right\rfloor\)
      • \(R/S\times B^k=v\)
      • \(M^-/S\times B^k=v-v^-\)
      • \(M^+/S\times B^k=v^+-v\)
  • 手順：
    • \(R\leftarrow f\times b^{\max\{e-p,0\}}\) （※\(b=2\)ならビットシフトが利用できる）
    • \(S\leftarrow b^{\max\{0,-(e-p)\}}\) （※\(b=2\)ならビットシフトが利用できる）
    • （ここで\(R/S=f\times b^{e-p}=v\)が成り立つ）
    • \(M^-\leftarrow b^{\max\{e-p,0\}}\) （※\(b=2\)ならビットシフトが利用できる）
    • \(M^+\leftarrow M^-\)
    • （ここで\(M^-/S=M^+/S=b^{e-p}\)が成り立つ）
    • \(f=b^{p-1}\)の場合（筆者注：非正規化数を考慮する場合は、「かつ、\(e\ne\mathit{emin}+1\)の場合」）
      • \(M^+\leftarrow M^+\times b\)
      • \(R\leftarrow R\times b\)
      • \(S\leftarrow S\times b\)
      • （ここでは実質的に\(M^-\)を\(b\)で割っている。\(f=b^{p-1}\)の場合は隣の浮動小数点数とのギャップが左右で異なるため）
    • （ここで\(R/S=v\), \(M^-/S=v-v^-\), \(M^+/S=v^+-v\)が成り立つ）
    • \(k\leftarrow 0\)
    • 以下ループ：
      • （不変条件：\(R/S\times B^k=v\), \(M^-/S\times B^k=v-v^-\), \(M^+/S\times B^k=v^+-v\)）
      • \(R<\lceil S/B\rceil\)の場合：
        • \(k\leftarrow k-1\)
        • \(R\leftarrow R\times B\)
        • \(M^-\leftarrow M^-\times B\)
        • \(M^+\leftarrow M^+\times B\)
      • そうでない場合（\(R\ge S/B\)）はループから抜ける
    • （主張：\(k=\min\{0,1+\lfloor\log_B v\rfloor\}\), \(B^{k-1}\le v<\frac{v+v^+}{2}\)）
    • 以下ループ：
      • （不変条件：\(R/S\times B^k=v\), \(M^-/S\times B^k=v-v^-\), \(M^+/S\times B^k=v^+-v\)）
      • \(2\times R+M^+\ge 2\times S\)の場合：
        • \(k\leftarrow k+1\)
        • \(S\leftarrow S\times B\)
      • そうでない場合（\(2\times R+M^+<2\times S\)）はループから抜ける
    • （主張：\(k=1+\left\lfloor\log_B\frac{v+v^+}{2}\right\rfloor\), 言い換えれば\(B^{k-1}\le\frac{v+v^+}{2}<B^k\)）

出力パート：

  • 入力：
    • 準備パートの出力\(k\), \(S\), \(R\), \(M^+\), \(M^-\)
  • 出力：
    • 整数\(H\), \(N\), \(D_i\) (\(N\le i\le H\))
  • 手順：
    • \(H\leftarrow k-1\)
    • \(R_{H+1}:=R\)
    • \(M^-_{H+1}:=M^-\)
    • \(M^+_{H+1}:=M^+\)
    • ループ：
      • （不変条件：\(R_k/S\times B^k+\sum_{i=k}^H D_i\times B^i=v\)）
      • \(k\leftarrow k-1\)
      • \(U_k:=\lfloor R_{k+1}\times B/S\rfloor\)
      • \(R_k:=(R_{k+1}\times B)\bmod S\)
      • （ここで\(R_{k+1}\times B=U_k\times S+R_k\)が成り立ち、帰納的に\(R_k=R\times B^{H+1-k}-\sum_{i=k}^H U_i\times B^{i-k}\times S=v\times S\times B^{-k}-\sum_{i=k}^H U_i\times B^{i-k}\times S\)が成り立つ）
      • \(M^-_k:=M^-_{k+1}\times B\)
      • \(M^+_k:=M^+_{k+1}\times B\)
      • （ここで\(M^-_k=M^-\times B^{H+1-k}\), \(M^+_k=M^+\times B^{H+1-k}\)が成り立つ）
      • \(\mathit{low}\leftarrow 2\times R_k<M^-_k\)
      • \(\mathit{high}\leftarrow 2\times R_k>2\times S-M^+_k\)
      • 解説：（★）
      • \(\mathit{low}\)と\(\mathit{high}\)で場合分け：
        • いずれも偽の場合：出力\(D_k:=U_k\)とし、ループを継続。
        • \(\mathit{low}\)が成り立ち、\(\mathit{high}\)が成り立たない場合：出力\(D_k:=U_k\)とし、ループを抜ける。
        • \(\mathit{high}\)が成り立ち、\(\mathit{low}\)が成り立たない場合：出力\(D_k:=U_k+1\)とし、ループを抜ける。
        • いずれも真の場合：
          • \(2\times R<S\)の場合は出力\(D_k:=U_k\)とし、ループを抜ける。
          • \(2\times R>S\)の場合は出力\(D_k:=U_k+1\)とし、ループを抜ける。
          • \(2\times R=S\)の場合は出力\(D_k\)は\(U_k\)または\(U_k+1\)とし、ループを抜ける。
    • \(N:=k\)とする。

（★）の部分で何が起こっているか詳しく見てみる。

\(\tilde{U}_k:=\sum_{i=k}^H U_i\times B^i\)とおく。これは\(v\)の\(B\)進での仮の近似小数である。すると、\(\tilde{U}_k+R_k/S\times B^k=v\)（ループ不変条件）であり、\(\tilde{U}_k\le v<\tilde{U}_k+B^k\)である。この状況を数直線上に表すと以下のようになる：

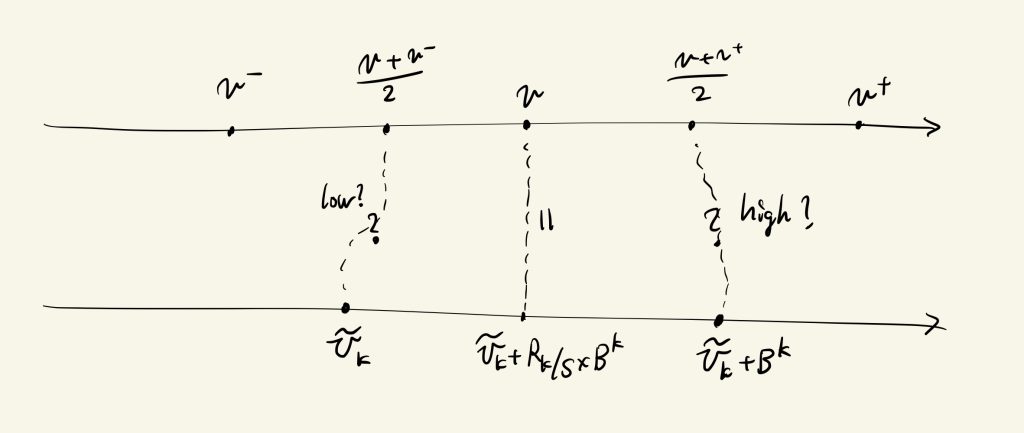
得たいのは、\(\frac{v+v^-}{2}\)と\(\frac{v+v^+}{2}\)の間に収まる\(B\)進近似小数である。ここでもし\(\frac{v+v^-}{2}<\tilde{U}_k\)であれば、\(\tilde{U}_k\le v\)と合わせて、\(\tilde{U}_k\)が条件を満たす。あるいは、\(\tilde{U}_k+B^k<\frac{v+v^+}{2}\)であれば、\(v<\tilde{U}_k+B^k\)と合わせて、\(\tilde{U}_k+B^k\)が条件を満たす。

つまり、\(\mathit{low}:\Leftrightarrow \frac{v+v^-}{2}<\tilde{U}_k\), \(\mathit{high}:\Leftrightarrow \tilde{U}_k+B^k<\frac{v+v^+}{2}\)とおいて、\(\mathit{low}\)または\(\mathit{high}\)が成り立てば、ループを脱出して良いことになる。

この条件\(\mathit{low}\)および\(\mathit{high}\)をそれぞれ整数の言葉で書き直せば、アルゴリズム中に記述した条件となる。

条件が両方成り立てば、近似小数\(\tilde{U}_k\)と\(\tilde{U}_k+B^k\)の両方が適格ということになるが、その場合は\(v\)に近い方を選ぶ。両方等距離ならば、「四捨五入」とか「最近接偶数丸め」とかの基準で選べば良い。

このエントリーをはてなブックマークに追加

“浮動小数点数の文字列化（基数変換）” に1件のフィードバックがあります

  1. ピンバック: LunarML進捗・2022年4月 | 雑記帳

コメントは停止中です。