最近(ここ半世紀くらい)圏論が流行りですね。しかし圏論は抽象的で、具体例や圏論の言葉を使うことによるメリットが見えないと、なかなかとっつき難いかもしれません。
この記事では、高校数学に出てくるアレが、実は圏論の言葉でスッキリ(?)表せることを見てみます。
予備知識:高校数学、若干の圏論、あとは多変数の微分の知識があればなお良い
目次
合成関数の微分
\(\def\Real{\mathbf{R}}\)実数\(\Real\)上の関数 \(f,g\colon\Real\to\Real\) の合成関数 \(g\circ f\) の微分は、\[(g\circ f)'(x)=g'(f(x))f'(x)\]と書けます。あるいは、\(y=f(x)\), \(z=g(y)\) とおけば\[\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}\]と書くこともできます。高校で習ったと思いますが、これを連鎖律と呼ぶのでした。
連鎖律は \(dx\), \(dy\), \(dz\) とかで書けば分数っぽく見えて美しいのですが、 \(f\), \(g\) をそのまま使った表記では、 \(g’\) の中に \(f\) がいてややこしいですね。合成関数というくらいですから、関数 \(f\), \(g\) を活かした表記を使いつつ、連鎖律をもっとスッキリ書けないでしょうか。
合成関数の微分:多変数の場合
本題に入る前に、連鎖律を多変数の場合に一般化しておきましょう。
多変数ベクトル値関数 \(f\colon\Real^n\to\Real^m\), \(g\colon\Real^m\to\Real^l\) の合成 \(g\circ f\colon\Real^n\to\Real^l\) を考えます。ただし、\(f\), \(g\) それぞれの成分を \[f(x)=\begin{pmatrix}f_1(x)\\\vdots\\f_m(x)\end{pmatrix},\quad g(y)=\begin{pmatrix}g_1(y)\\\vdots\\g_l(y)\end{pmatrix}\]とおきます(値の方は縦ベクトルだと思います)。
合成関数 \(g\circ f\) の微分(連鎖律)は、偏微分の記号を使うと\[\frac{\partial(g\circ f)}{\partial x_i}(x)=\sum_{j=1}^m\frac{\partial g}{\partial y_j}(f(x))\frac{\partial f_j}{\partial x_i}(x)\]と書けるのでした。
多変数の場合は一変数の場合と比べてもややこしくなってしまいました。しかし、ヤコビ行列\[Jf(x)=\begin{pmatrix}
\frac{\partial f_1}{\partial x_1}&\cdots&\frac{\partial f_1}{\partial x_n}\\
\vdots&&\vdots\\
\frac{\partial f_m}{\partial x_1}&\cdots&\frac{\partial f_m}{\partial x_n}
\end{pmatrix},\quad Jg(y)=\begin{pmatrix}
\frac{\partial g_1}{\partial y_1}&\cdots&\frac{\partial g_1}{\partial y_m}\\
\vdots&&\vdots\\
\frac{\partial g_l}{\partial y_1}&\cdots&\frac{\partial g_l}{\partial y_m}
\end{pmatrix}\]を導入すると、合成関数の連鎖律は次のように書けます:\[J(g\circ f)(x)=Jg(f(x))Jf(x)\]ただし、右辺は行列の積です。
こうしてみると、多変数の場合の連鎖律は、一変数の場合のプライム \({}’\) をヤコビ行列の \(J\) に置き換えたものであることがわかります。ここでも、 \(Jf\) の中に \(g\) がいてややこしいですね。
圏の言葉
\(\def\VectFin{\mathbf{Vect}^{\mathrm{fin}}_\Real}\)連鎖律を圏の言葉で表すために、いくつかの圏を定義します。まず、\(\mathcal{C}\) は
- 対象:自然数 \(n\) について \(\Real^n\) 、つまり集まりとしては \(\{\Real^n\mid n\in\mathbf{N}\}\)
- 射:微分可能な関数 \(\Real^n\to\Real^m\)
からなる圏です。
次に、\(\VectFin\) は
- 対象:自然数 \(n\) について \(\Real^n\) 、つまり集まりとしては \(\{\Real^n\mid n\in\mathbf{N}\}\)
- 射:線形写像 \(\Real^n\to\Real^m\)、あるいは行列と言っても良い。射の合成は行列の積となる
からなる圏です。(雑な定義だ!と思った方は黙っていてください)
\(\mathcal{C}\) と \(\VectFin\) は(ここでの定義では)同じ対象からなりますが、射が異なるので全く異なる圏です。
そしてもう一つ、 \(\mathcal{C}\) の点付きバージョン \(\mathcal{C}_*\) を次のように定義します:
- 対象:\(\mathcal{C}\) の対象 \(U\) と、 \(U\) の点 \(a\) からなる組 \((U,a)\)
- 射 \((U,a)\to(V,b)\):\(\mathcal{C}\) の射 \(f\colon U\to V\) であって、点 \(a\) を点 \(b\) に写すもの(\(f(a)=b\) を満たすもの)
これはコンマ圏の一種ですが、コンマ圏についてはここでは解説しません。
微分と関手
圏 \(\mathcal{C}_*\) から圏 \(\VectFin\) への対応 \(T\) を、次のように定めます:
- 対象の対応:\((U,a)\) を、 \(\Real^n\) に写す(ただし \(n=\dim U\))
- 射の対応: \(f\colon(U,a)\to(V,b)\) を、行列 \(Jf(a)\) で表される線形写像 \(\Real^n\to\Real^m\) に写す(ただし \(n=\dim U, m=\dim V\))
この対応は、関手になります。つまり、 \(\mathcal{C}_*\) の恒等射 \(\mathrm{id}_{(U,a)}\colon(U,a)\to(U,a)\) に対して対応 \(T\) は \(\VectFin\) の恒等射(つまり単位行列)を対応させ、\(\mathcal{C}_*\) の合成関数を \(\VectFin\) の合成関数に対応させます:\[T(\mathrm{id})=\mathrm{id},\quad T(g\circ f)=Tg\circ Tf.\]
確認していきましょう。
\(\mathcal{C}_*\) での \(\mathrm{id}\) は\[\begin{array}{cccc}\mathrm{id}\colon&(U,a)&\longrightarrow&(U,a)\\&\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}&\longmapsto&\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}\end{array}\]ですから、その偏微分は\[\frac{\partial}{\partial x_i}\mathrm{id}=\begin{pmatrix}0\\\vdots\\1\\\vdots\\0\end{pmatrix}\text{($i$番目だけが1)}\]で、ヤコビ行列は\[J\mathrm{id}(a)=\begin{pmatrix}1&&0\\&\ddots&\\0&&1\end{pmatrix},\]つまり単位行列となります。\(\VectFin\) での恒等射は単位行列なので、確かに \(T\) は単位行列を単位行列に移すことがわかりました。
次に、\(T\) が \(\mathcal{C}_*\) での射の合成(合成関数)を \(\VectFin\) での射の合成(行列の積)に移すことを見ましょう。
\(f\colon(U,a)\to(V,b)\) と \(g\colon(V,b)\to(W,c)\) の合成 \(g\circ f\colon(U,a)\to(W,c)\) を考えます。定義より \(T(g\circ f)=J(g\circ f)(a)\) ですが、この右辺は連鎖律より \(J(g\circ f)(a)=Jg(f(a))Jf(a)\) なのでした。\(\mathcal{C}_*\) の射の定義より \(f(a)=b\) で、行列の積は \(\VectFin\) での射の合成なので、\(Jg(f(a))Jf(a)=Tg\circ Tf\)です。つまり\[\begin{aligned}T(g\circ f)&=J(g\circ f)(a)\\&=Jg(f(a))Jf(a)\\&=Jg(b)Jf(a)\\&=Tg\circ Tf\end{aligned}\]で、\(T\) は射の合成を射の合成に写します。
これで、 \(T\) が確かに関手であることを確認できました。
ここで、 \(T\) を関手たらしめるものは何だったかと振り返ってみると、それは微分の連鎖律であったことがわかります。標語的に言えば「微分は関手であり、連鎖律は関手性である」となるでしょうか。知ったかぶりをしたい人はこの標語だけ覚えて帰ってください。
まとめ
微分の連鎖律とは\[T(g\circ f)=Tg\circ Tf\]のことである。
微分と関手と直積
先ほど定義した \(T\) は直積を保ちます。つまり、 \(\mathcal{C}_*\) での直積の図式\[A\stackrel{\mathrm{pr}_1}{\longleftarrow}A\times B\stackrel{\mathrm{pr}_2}{\longrightarrow}B\]を \(T\) で写したもの\[TA\stackrel{T\mathrm{pr}_1}{\longleftarrow}T(A\times B)\stackrel{T\mathrm{pr}_2}{\longrightarrow}TB\]もまた、(\(\VectFin\) において)直積の図式となります。つまり \(T(A\times B)\cong TA\times TB\) です。
応用
例えば、次の関数 \(f\) の微分を計算したいとします:\[f(x,y)=\left(\frac{\exp(x)}{\exp(x)+\exp(y)},\frac{\exp(y)}{\exp(x)+\exp(y)}\right)\]この関数は、次の図式のように「足し算」「割り算」「指数関数」の合成で書けます(割り算の定義域は0を除きますが、そこは目をつむってください)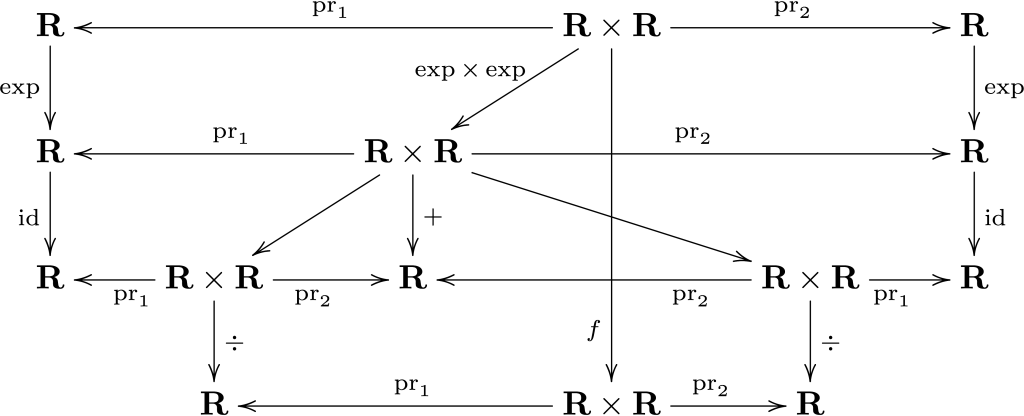
先ほどの標語では「微分は関手」なので、この \(f\) の微分を計算するには、それを構成するパーツ、つまり足し算、割り算、指数関数などの微分を計算し、合成してやれば良い(つまり、図式を関手で写す)のです。この際に二変数関数 \(\Real\times\Real\to\Real\) があってもうまくいくことを保証するのが、「関手が積を保つ」という性質です。
この考え方を応用すると、プログラミング言語で実装した数学関数を、使っている演算(\(+\) や \(\times\), \(\exp\))を機械的に置き換えることで、関数の微分を計算できます。
もっと詳しく知りたい方へ
この記事での圏 \(\mathcal{C}\) の定義は大雑把で、例えば原点で定義されない関数 \(f(x)=\frac{1}{x}\) を取り扱えません。その辺の話をもう少し拡張したい、一般化したいという方は多様体論を勉強してください。
多様体論では接平面 (tangent space) というものが出てきますが、それがこの記事で言う「\(\mathcal{C}_*\) の対象を \(\VectFin\) の対象に移す対応」です。射の対応も含めて関手として取り扱う場合は tangent functor (訳すなら「接関手」でしょうか)と呼ばれるようです。ネタバラシをすると、この記事で関手に \(T\) と名付けたのは、 Tangent space / Tangent functor の T を意図したものでした。
プログラミングとの関連は 逆伝播 自動微分などのキーワードで調べてください。俺は知らん。
リンク:

とても分かりやすかったです(^○^)