もしもそれがTeX言語を受理し、TeXのように動くのであれば、それは紛れもない
クソである — 詠み人知らず
前回の記事に書いたようなLaTeX数式をMathMLに変換するやつを、自分で実装したい。そのためには、マクロの展開など、TeXの挙動を真似ることが必要である。
この記事では、TeXのようなものを作るにあたって感じるTeXのアレな点や、気になる拡張機能を挙げていきたい。
全体的に、TeXの重箱の隅のような話題をまとまりもなく書き連ねているので、読み物としてはよろしくないかもしれない。
目次
\csnameの副作用
TeXのコマンドのうち、展開可能コマンドと呼ばれるものは基本的に展開器の状態をいじってトークン列を生み出す以外の副作用は起こさない。だが、\csnameだけは異なる。
\csnameは、生み出した制御綴が未定義ならば、その制御綴が\relaxと等価になるように定義する。つまり、\fooが未定義の状態で
\csname foo\endcsname \foo
を実行してもエラーとはならず、\fooが\relaxと等価になる。
制御綴が定義済みかどうか確かめるために\csnameを使う場合、この副作用が邪魔になることがある。
この副作用を抑え込むために、\expandafterを使ったトリックがある:
\begingroup\expandafter\expandafter\expandafter\endgroup \expandafter\ifx\csname foo\endcsname\relax ...
ちなみに、e-TeXでは、このようなトリックを使わなくても制御綴が定義済みかどうかテストできるコマンドを用意している:
\ifdefined \ifcsname
TeXっぽいものを実装する側からすると、展開可能コマンドとそれ以外のコマンドを型レベルで区別する場合に\csnameの副作用が邪魔になる。
「型レベルで区別」というのがどういうことかというと、Haskell風の疑似コードで書いた時に
data Value = ExpandableCommand (State -> ([Token], ExpansionState))
| Command (State -> State)
| ...
data State = State { expansionState :: ExpansionState
, definition :: Map CommandName Value
, ...
}
という感じで、通常の「展開可能コマンド」は展開器の状態だけを更新する(戻り値で展開器の新しい状態を返す)関数として実現できる。一方で、\csnameは制御綴から値への対応を変更するという副作用を持つため、そういう関数として書くことができない。
\noexpand
「\noexpandされたトークンは\relaxと等価になる」ということになっているが、そうでもない。
次のコードは、1行目で\noexpand\bazというトークン列を1回展開したものを\fooに代入する:
\expandafter\let\expandafter\foo\noexpand\baz
\ifx\foo\relax\message{yes}\else\message{no}\fi
\show\foo
2行目ではそれ(\foo)が\relaxと等価かどうかを\ifxでテストして、3行目では\fooの中身を表示する。
「\noexpandされたトークンが\relaxと等価になる」のであれば、2行目のテストではyesが出力され、3行目では \foo=\relax. が出力されるはずである。
やってみると、3行目では期待通りに \foo=\relax. となるが、2行目ではnoが出力される。つまり、\noexpandで生成されるのは「\showの意味では\relaxと等価だが、\ifxの意味では\relaxと等価ではないナニカ」である。
なお、上記のコードをLuaTeX 1.0.4 (TeX Live 2017)で実行したところ、\showの結果が \foo=\relax. ではなくて
\foo=[unknown command code! (0, 1)].
となった。多分LuaTeXのバグだろう。
関連リンク:tex core – \ifx doesn’t treat \noexpand as \relax – TeX – LaTeX Stack Exchange
分数と\mathchoice
LaTeXでの分数 \frac は、 \frac{1}{2} という風に、コマンド名の後に分子と分母が続く。しかし、plain TeXで分数を書くのに使う \over は、 {1 \over 2} という風に中置で使う。
(ちなみに、LaTeXの\fracコマンドは内部的には\overによって実装されている。)
普通のマークアップ言語やプログラミング言語だったら、演算子が中置であっても何の問題もない。しかし、TeXは前から順に処理をする言語であり、前の部分を実行しないことには後の部分を字句解析することすらできない。つまり、分子の処理をしている段階では、処理対象が分数の分子であるということはわからない。
さて、通常のディスプレイ数式と分数の分子の中では、数式スタイルが変わる。
TeXは組版用の言語なので、現在の数式スタイルに応じて挙動が変わるようなTeXコードを書けても不思議ではない。
実際、\mathchoiceコマンドを使うと数式スタイルに応じて内容を変えることができる。しかし、実行の時点では数式スタイルは確定していないため、\mathchoiceは4つの数式スタイル全てに着いて実行・組版して、その後確定した数式スタイルに応じて実際に出力する内容を決める、という動作をするらしい。ヤバい。The TeXbookにも「\mathchoiceはコストが高いから注意しろよ」的なことが書かれている。
参考:
さて、LuaTeXでは\mathstyleというプリミティブを導入して、より直接的に「現在の数式スタイル」を取得できるようになっている。
こうなると当然、分数の分子のところでは正しい数式スタイルが取得できない。そこで、LuaTeXでは\Ustackというプリミティブを導入し、分数の開始を明示できるようになっている。
つまり、
\Ustack {分子 \over 分母}
と書くことによって「分子」の部分で正しい数式スタイルが得られるようになる。
参考:
ということは、LaTeXの\fracの定義を\Ustackを使うように変えれば、分数の分子でも\mathstyleで正しい数式スタイルを得ることができる。残念ながらLaTeXの\fracコマンドは標準では\Ustackを使わないので、外部のパッケージを読み込む必要がある。
一方、(ソースを斜め読みした限りでは)ConTeXtでは\Ustackを使うようになっているようである。(ConTeXtはLuaTeXに全面的に依存しており、LuaTeXの機能をConTeXtが使わなかったら誰が使うのか、という話である。ちなみにLuaTeXのマニュアルはConTeXtで書かれている。)
さて、TeXらしきものを新しく実装するにあたって、\mathchoiceを「4回実行する」ように実装する必要があるのか、という問題がある。
想定する入力は「LaTeX数式」であり、\fracや\Ustackを介さずに\overを直接使うような愚かな入力は拒否しても良いだろう。そうすると数式スタイルは実行時に確定するはずで、\mathchoiceの4つの選択肢のうち1つだけを実行するという実装が可能になる。
しかし、そのような挙動はTeXの仕様に反するので、既存のパッケージ類はそのままでは動かなくなる可能性がある。実際、amstextは\mathchoiceの挙動を前提として対策を打っているので、もしも\mathchoiceの挙動を変えるのであればパッチが必要になる。
プリミティブの拡張
現代使われているTeX処理系は、KnuthのオリジナルのTeXと比べて色々な拡張機能が実装されている。自分でTeX互換処理系を作る場合には、そのような拡張機能を実装すると面白いだろう。
例えばe-TeXには\ifdefinedや\ifcsnameという拡張機能があることはすでに書いた。このほか、比較的馴染み深いであろうe-TeX拡張としては\middleがある。
LuaTeXの\mathstyleと\Ustackも既に述べた。
pdfTeXも多数のプリミティブを提供している。組版機能とは関係ない拡張としては例えば、\ifincsnameや\pdfstrcmpなどがある。
pdfTeXのこのような便利なプリミティブの一部は、XeTeXやe-pTeXにも移植されている。
Unicode
LaTeX数式をMathML等に変換するにあたっては、\sum等の記号を ∑ (U+2211 N-ARY SUMMATION) のようなUnicode文字に対応させることになる。つまり、TeXもどきを実装するにあたっては、Unicodeを意識する必要がある。
しかし、オリジナルのTeXはUnicodeが影も形もない時代に作られており、内部的な文字コードはせいぜい8ビットで、Unicodeの21ビットとは大きな開きがある。
一方、LuaTeXとXeTeX等のモダンな処理系はネイティブにUnicodeに対応しており、\Umathcode等のプリミティブによってUnicodeコードポイントに対してmathcode等を割り当てることができる。
MathMLを出力するTeX処理系を作る場合には、このような\Umath系プリミティブの機構を参考にすると良いかもしれない。
ところで、LaTeXとUnicodeと言えばunicode-mathパッケージである。Unicodeを意識したTeXもどきを実装する際にはunicode-mathを参考にすると良いかもしれない。
Unicodeつながりでもう一つ。TeXには制御文字を記述するための ^^ という記法があるが、LuaTeXはこの記法を拡張してUnicodeコードポイントをASCII文字のみで入力できるようにしているようだ。つまり、
- ^^の後に1文字(TeXの機能)
- ^^の後に16進2桁(TeXの機能)
- ^^^^の後に16進4桁(LuaTeXの機能)
- ^^^^^^の後に16進6桁(LuaTeXの機能)
によって制御文字またはUnicodeコードポイントを入力できる。16進数を書く場合は小文字で書く必要がある。
例:
$ luatex
This is LuaTeX, Version 1.0.4 (TeX Live 2017)
restricted system commands enabled.
**\message{^^^^^^01f600}
😀
数式中のカッコの対応
前回もちょろっと書いた気がするが、LaTeX数式をMathMLに変換する際は、カッコの対応を取らなくてはならない。
素朴には\mathopenを開きカッコ、\mathcloseを閉じカッコと思って対応させるのが良さそうに思えるが、LaTeXではカッコ以外に ! と ? の数式クラスも\mathcloseになっている(後置演算子のつもりなのだろうか)。なので、数式クラスを見るだけではダメである。
ではどうするか。
まず、\left \rightは確実に「対応するカッコ」なので、そこを優先的に対応させるべきだろう。
次に、\bigl\bigrのようなカッコの大きさを変えるやつが使われている場合は、同じ大きさのものを対応させるのがよいだろう。
最後に\mathopen, \mathcloseの対応を見るわけだが、カッコか後置演算子かの判別にはdelimiter codeが使えそうな気がする。
まあまだ実際に実装したわけではないので、この方針がうまくいくかどうかはわからない。
余談
ConTeXtにはMathMLで数式を記述する機能があるようだ。MathMLはXMLなので手書きに向いているとは言いづらいが、同じソースからPDFとHTMLを出力する目的であればそういう方向性も割と合理的かもしれない。ただ、この記事および前回の記事は「LaTeX数式をMathMLに変換したい」という、真逆の趣向である。


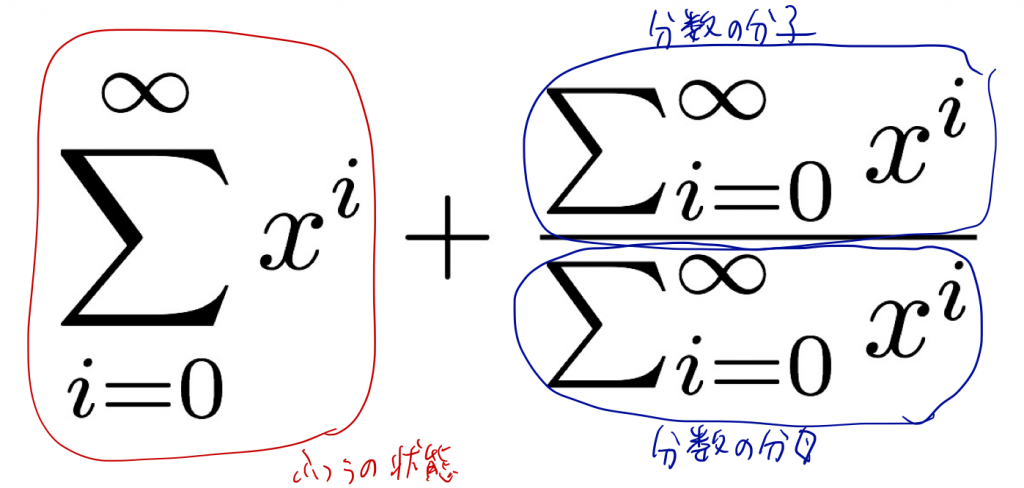
ピンバック: LaTeX数式 to MathML を考える その2 | 雑記帳
ピンバック: 「正しいmathstyle」を求めて | 雑記帳
ピンバック: TeX言語のトークンと値 その2:noexpandと、挿入されたrelax | 雑記帳
ピンバック: 2018年振り返り | 雑記帳