【2017年12月18日 追記】この記事は古いTypeScript (2.0以前) を念頭に置いている。もちろん、現在のTypeScriptにも当てはまる記事はあるだろうし、TypeScript以外の言語における合併型 (union types) についてもある程度読み替えられるかもしれない。ただしElmとは “Union Types” の用法が完全に相入れないのでElmユーザーの方はお帰りください。
TypeScript 1.4について、 TypeScript 1.4.1 変更点 – Qiita という記事が目に留まった。で、その中の
直和型(Union Types)
という項目に引っかかりを感じた。:
なぜ引っかかりを感じたかというと、TypeScriptに今回導入されたUnion Typesと、巷に言う直和型というのは、異なる概念であるからだ。
注意:以下の話は型理論の専門家でもないフツーの学生が適当に書いた程度の信憑性しかありません。
余積としての直和型
まず「直和型」(sum type)の定義だが、ここではTypeScriptの型と(一変数)関数のなす圏における余積(coproduct)とする。といっても、あまり細かいことは気にしない。
圏の余積はどういうものだったか思い出してみよう。対象 \(A\) と \(B\) に対する \(A\) と \(B\) の余積(coproduct) \(A\sqcup B\) とは、射 \(\mathrm{inl}\colon A\to A\sqcup B\) (left injection)と射 \(\mathrm{inr}\colon B\to A\sqcup B\) (right injection)があって、任意の対象 \(C\) と 射の組 \(f\colon A\to C, g\colon B\to C\) に対して次の図式を可換にする射 \(A\sqcup B\to C\) が一意的に存在するもののことであった。
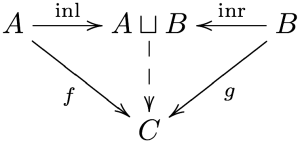
数学における例を出すと、集合の非交和は集合の圏における余積となっている。
具体的なプログラミング言語における直和型の例としては、Haskellだと Either a b が a と bの直和型となっている。\(\mathrm{inl}\) は型構築子 Left :: a → Either a b、\(\mathrm{inr}\) は型構築子 Right :: b → Either a b である。
C言語のいわゆる「タグ付きunion」も直和型と言える。
注意してほしいのは、直和型は、一般には「左右どちらの値を持っているか知っている」という点である。たとえ \(A=B\) であっても、\(A\) と \(A\sqcup B(=A\sqcup A)\) は一般には別の型である。(注:ただし、\(A\) が始対象であれば \(A\) と \(A\sqcup A\) は同型になる)
部分型とunion type
型 B が型 A の部分型(subtype)であるとは、型 B の値が型 A の値としてもみなせるということである。
例えば、(適切な例と言えるかは自信がないが)C言語では int 型の値は double 型の値としてもみなせる(double 型の値を必要とする文脈で使える)。すなわち、int 型は double 型の部分型である。
あるいは、典型的なオブジェクト指向言語で class Derived : public Base という感じでクラスの継承関係があれば、Derived 型の値は Base 型の値としてもみなせる。すなわち、Derived 型は Base 型の部分型である。
部分型(subtype)の逆の関係をsupertype(しっくりくる訳語が浮かばなかった 「型システム入門」では上位型と訳している)という。例えば、TypeScriptでは、any はあらゆる型のsupertypeである
【2017年12月18日 追記】TypeScriptの any は漸進的型付け (gradual typing) との関係があって特殊なので、ここで例示するのは適当ではないかもしれない。単にあらゆる型の supertype というだけであれば {} が相応しいと思われる。【ここまで追記】
このように、型システムに部分型(subtyping)が定まっていることを前提とすれば、TypeScriptに導入された union type というのは、以下の3条件を満たす型であると言える。(一方で、直和型は部分型に関係なく定義できる)
A|BはAのsupertypeである。つまり、型Aをもつ値は型A|Bの値としてもみなせる。A|BはBのsupertypeである。つまり、型Bをもつ値は型A|Bの値としてもみなせる。CがAのsupertypeであると同時にBのsupertypeであるならば、CはA|Bのsupertypeである。
特に、A と A 自身のunion type A|A はもとの A と全く同じ型になる。(直和型について、\(A\) と \(A\sqcup A\) が一般には別の型になることとは対照的だ)
数学で言う集合の和集合(union)と同じような感じだ。
順序集合になじみのある人向けの言葉で言えば、TypeScriptの型を、部分型関係(subtyping relation)を射として圏(前順序の圏)とみなしたときの余積である。
まとめ
直和型とunion typeというのは、どちらも、型を対象とする圏の余積にはなっているが、考えている圏が違う。なのでこれらは違う概念である。
↓読み手を混乱させる駄文
ただし、集合 \(A\) と \(B\) の共通部分が空の時に和集合 \(A\cup B\) は集合の直和(非交和)にもなっていた。同様に、型 A と型 B の「共通の値」が存在しないのであれば、union type A|B は直和型とみなすこともできるだろう。
が、TypeScriptには null や undefined という、「任意の型に当てはまる値」があるので、A|B は直和型にはならない。
【2017年12月18日 追記】TypeScript 2.0で導入された --strictNullChecks の下では、 null や undefined は「任意の型に当てはまる値」ではなくなった。【ここまで追記】
逆に言えば、 null や undefined の存在を無視すれば、例えば number|string は number と string の直和型だとみなせる。
しかし、個々の場合に直和型になる場合があったとしても、一般にはunion typeは直和型ではないという結論に変わりはない。
↑読み手を混乱させる駄文
おまけ
【2017年12月18日 追記】TypeScript 2.0で正式に tagged union types (または discriminated union types) が導入された。これは、文字列リテラル型のフィールドを含む型の合併 (union) によって直和型を実現する。以下に書くコードは TypeScript 1.4 の時代に筆者が遊びで書いたものであり、2017年現在採用するべき方法ではない。【ここまで追記】
じゃあTypeScriptでの直和型って何なのよ?っていうと、例えば次のような感じで実装できる。(深く考えていないのでマズい点があるかもしれない)
