対数関数や平方根のような複素関数は、閉曲線に沿って解析接続すると元の関数と値がずれる場合がある。対数関数や平方根であればまだ単純だから良いが、根号の中に多項式等が入るような関数だと、具体的な曲線に対して関数の枝(ブランチ)を計算するのは少し面倒である。

というわけで、以前に作った複素積分の Web アプリ（ブラウザアプリ）のような感じで、平面に描いた曲線に沿って解析接続してくれるアプリ（Web ページ）を作った。「複素関数で遊ぼう」「たのしい複素積分」に続く、複素関数シリーズ第3弾とでも言おうか。今のところ愛称は設定していないが、気が向いたらページのタイトルを「わくわく解析接続」に変えているかもしれない。→変えた。この記事のタイトルも変更。

URL: https://miz-ar.info/webapp/analytic-continuation/

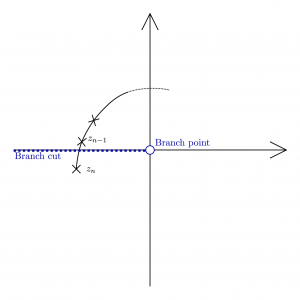
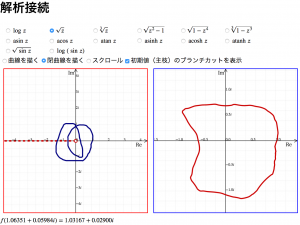解析接続と言っても、定義通りに級数を再展開するようなことはしていなくて、単純に、「曲線が branch cut を跨いだら枝(ブランチ)を切り替える」ように処理しているに過ぎない。

対数関数の主値を \(\DeclareMathOperator{\Log}{Log}\Log z\) で書くと、他の枝の値は整数 \(n\) を使って \(\Log z + 2n\pi i\) と書ける。曲線が branch cut をまたぐ毎に、この \(n\) を増減してやれば良い。

平方根の場合は、主値が \(\sqrt{z}\) ならもう一つの枝の値は \(-\sqrt{z}\) なので、曲線が branch cut をまたぐ際に符号を反転させる。\(n\) 乗根の場合は符号を反転させる代わりに \(e^{\frac{2\pi i}{n}}\) をかける。

逆三角関数や逆双曲線関数は、対数関数や平方根を使って定義できるので、枝の切り替えを考慮した合成関数として実装してやれば良い。

曲線の始点での値（初期値）の計算には、その関数の（恣意的に選ばれた）主値が使われる。詳しくは、前回の記事を見て欲しい。Branch cut の位置は、画面のチェックボックスにチェックを入れると点線として表示させることができる。

逆双曲線関数と逆三角関数の branch cut

今のところ、関数はあらかじめ用意されたものの中から選ぶだけとなっている（自分で数式を入力できない）が、「この関数を実装してほしい」というような要望があれば、ここのコメント欄にでも書き込んでほしい。

関連

「たのしい複素積分」

https://miz-ar.info/math/singularity/

紹介記事：

たのしい複素積分

ユーザーインターフェースおよびソースコードの多くは「たのしい複素積分」のコピーである。なので、最初のプロトタイプは3時間くらいでできた。（その時は関数の種類も最低限で、「関数の像を平面に表示する」という機能もなかったが）

「複素関数で遊ぼう」

https://miz-ar.info/math/complex-functions/

複素平面に曲線を描いてそれを関数でうつした像を見るという機能としては、「複素関数で遊ぼう」も今回の Web ページも同じである。今回の Web ページで本質的に異なる点は、 branch cut をまたぐ際の挙動なので、そこに注目しながら比較してみて欲しい。