逆双曲線関数と逆三角関数をナメてかかっていたら落とし穴にはまったので、ブログ記事としてまとめておく次第である。

復習：実数の場合

逆双曲線関数

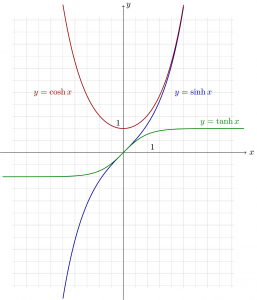
\(\DeclareMathOperator{\asinh}{asinh}\DeclareMathOperator{\acosh}{acosh}\DeclareMathOperator{\atanh}{atanh}\DeclareMathOperator{\asin}{asin}\DeclareMathOperator{\acos}{acos}\DeclareMathOperator{\atan}{atan}\newcommand\abs[1]{\left\lvert#1\right\rvert}\)双曲線関数は上の図のような感じなので、

• asinh: \((-\infty,\infty)\) で定義される1価関数。
• acosh: \([1,\infty)\) で定義される2価関数。典型的には値が正となるように選ぶ。
• atanh: \((-1,1)\) で定義される1価関数。

となる。これらは実数の対数と平方根を使って書くことができて、\begin{align*}
\asinh x&=\log\left(x+\sqrt{x^2+1}\right),&& \\
\acosh x&=\log\left(x\pm\sqrt{x^2-1}\right)=\pm\log\left(x+\sqrt{x^2-1}\right)&(x\ge1)&, \\
\atanh x&=\frac{1}{2}\log\left(\frac{1+x}{1-x}\right)&(\left\lvert x\right\rvert<1)&
\end{align*}となる。

逆三角関数

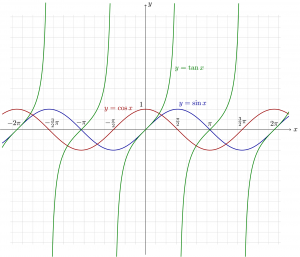
三角関数は上の図のような感じなので、

• asin: \([-1,1]\) で定義される無限多価関数。典型的には値を \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\) から選ぶ。
• acos: \([-1,1]\) で定義される無限多価関数。典型的には値を \([0,\pi]\) から選ぶ。
• atan: \((-\infty,\infty)\) で定義される無限多価関数。典型的には値を \(\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\) から選ぶ。

となる。

本題：複素数の場合

対数関数

複素数の対数関数は、実数の対数関数と偏角 arg を使うと次のように計算できる。\[\log z=\log\abs{z}+i\arg{z}.\]

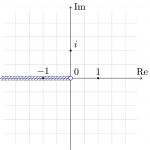
この偏角をどう取るかが問題になるが、その辺のプログラミング言語等では \(-\pi\) から \(\pi\) と取ることが多いので、ここでもそのように取る。つまり、定義域から実軸の負の部分を取り除き（下図）、一価正則な関数（枝; ブランチ）が得られる。この、取り除いた実軸の負の部分のことを branch cut と呼ぶ。“branch cut“ の日本語への定訳はなさそうである。

（プログラミング的には、定義域が開集合とかそういうこだわりはないので、実軸の負の部分を定義域から外すことはせず、単に実軸の負の部分で不連続な関数とする。また、浮動小数点数のゼロの符号を利用すると、偏角の範囲は \((-\pi,\pi]\) ではなく \([-\pi,\pi]\) となる。）

べき乗、平方根

複素数の対数関数を使うと、べき乗、平方根は次のように計算できる。枝は log の枝の選び方によって決まる。Branch cut も log のものに従う。\begin{align*}
z^w&=\exp(w\log z), \\
\sqrt{z}&=\exp\left(\frac{1}{2}\log z\right).
\end{align*}

今回の主題とは関係ないがついでなので書いておくと、この \(\sqrt{z}\) を実数の言葉で書くと次のようになる。\[\sqrt{x+iy}=\begin{cases}
\sqrt{\frac{x+\sqrt{x^2+y^2}}{2}}+\frac{iy}{\abs{y}}\sqrt{\frac{-x+\sqrt{x^2+y^2}}{2}} & y\ne 0 \\
\sqrt{x} & y=0, x\ge0 \\
\Bigl(\pm i\sqrt{-x} & y=\pm0, x<0\Bigr)
\end{cases}\]（ただし、コンピューターで浮動小数点数を使って計算する場合は桁落ちの問題があるので、この式の通りに計算してはいけない）

今回は実軸の負の部分を branch cut としているが、仮に log の別の枝を選んでも、対応するべき乗、平方根の枝は自然に定まる。

逆双曲線関数

実数の場合の式をそのまま使って\begin{align*}
\asinh z&=\log\left(z+\sqrt{z^2+1}\right), \\
\acosh z&=\log\left(z+\sqrt{z^2-1}\right)=\log\left(z+\sqrt{z^2-1}\right), \\
\atanh z&=\frac{1}{2}\log\left(\frac{1+z}{1-z}\right)
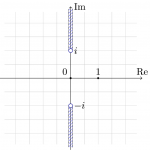
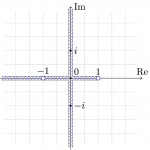
\end{align*}とすればOK。…と言いたいところだが、実用上はそういうわけにはいかない。これらの branch cut は次のようになる。

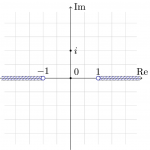
asinh, atanh の branch cut はこれで良いのだが、acosh の branch cut は少し過剰である。実軸上はともかく、虚軸に branch cut が入っているのは不必要に思える。虚軸の branch cut は \(\sqrt{z^2-1}\) が原因なので、符号を適当にかけて処理するとか、あるいはここを \(\sqrt{z+1}\sqrt{z-1}\) に変えるとかする。そうすると、次のような cut が入った acosh の枝が得られる。

（これらの逆双曲線関数の枝は、C言語で採用されているものと同一となる。）

逆三角関数

三角関数と双曲線関数の間には\begin{align*}
i\sin z&=\sinh(iz), \\
\cos z&=\cosh(iz), \\
i\tan z&=\tanh(iz)
\end{align*}という関係式があるので、逆三角関数は逆双曲線関数を使って\begin{align*}
\asin z&=-i\asinh(iz)=-i\log\left(iz+\sqrt{1-z^2}\right), \\
\acos z&=-i\acosh z=-i\log\left(z+\sqrt{z+1}\sqrt{z-1}\right), \\
\atan z&=-i\atanh(iz)=-\frac{i}{2}\log\left(\frac{1+iz}{1-iz}\right)
\end{align*}と書ける。…という単純な話では、もちろん、ない。

asin と atan はこれでいいのだが、acos が問題となる。複素数の逆三角関数を実数の逆三角関数の拡張として考えるならば、複素数の逆三角関数の定義域は実数の逆三角関数の定義域を含んでいてほしい。つまり、複素数の acos の定義域は実軸上の区間 \((-1,1)\) を含んでいてほしい。

だが、今使っている acosh の定義域は、実軸の1より小さいところに branch cut が入っているため、 acos を acosh の \(-i\) 倍により定義すると、実軸上の区間 \((-1,1)\) は定義域から外れてしまう！

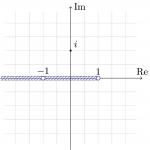
なので、acos は acosh を \(-i\) 倍するのではなく、別に考えてやらねばならない。例えば、\[\acos z=-i\log\left(z+i\sqrt{1-z^2}\right)\]とすると、これはちゃんと実数の acos の拡張となっていて、 branch cut は次のようになる。

（これらの逆三角関数の枝は、C言語で採用されているものと同一となる。）