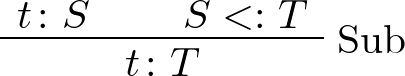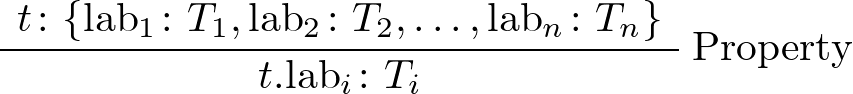前に書いた「TypeScript使いの憂鬱:never型はプロパティを持つか」の補足をして、関連する話題を取り上げます。前の記事では
「never型の式にプロパティアクセスができない」という動作は型システムの一貫性から外れた、アドホックな(場当たり的な)動作であるということです。
と書きました。「never型の式にプロパティアクセスができる」という動作が普通の型システムでどのように正当化されるのかを掘り下げます。
TAPLこと「型システム入門」をベースに説明します。
型付け可能性の定義
ある項(プログラム)に型がつくとはどういうことでしょうか?例えば、if true then 1 + 2 else 5 という項が正しく片付けされていることを確認するためには何があれば良いでしょうか?
普通の型システムでは、目的の項(と、その型)を結論とする導出木が存在することを以て、項が型付けされる、と定義すると思います。つまり、さっきの例なら
というような導出木が存在することによって、if true then 1 + 2 else 5 という項にNatという型がつくことが正当化されます(ここで使った規則の定義はしませんが、適宜脳内補完してください)。
集合の言葉で言うなら、「型付け関係は、所定の規則を全て満たす最小の二項関係である」(参考:「型システム入門」p71、定義8.2.1)となりますが、これは「導出木が存在する」と同じことです。
型システムに部分型付けがあっても原則は同じで、導出木が存在することによって型付けが正当化されるべきです。つまり、部分型付けの規則(包摂規則)
があって、never型が任意の型の部分型であるという規則
があって、オブジェクトのプロパティに関する規則
があれば、t : never に対して t.lab_i : T_i を結論とする導出木
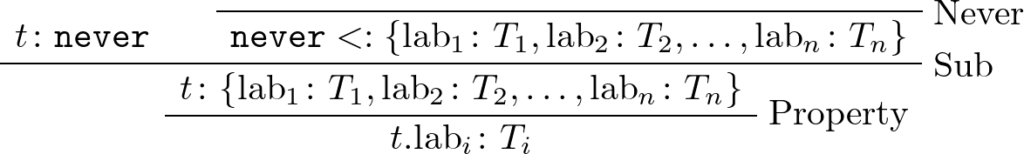
を構成できる(→存在する)ため、never型の項 t に対するプロパティアクセス t.lab_i は(任意の型について)型付けされるべきだ、ということになります。
これが、never型に対してプロパティアクセスが許容されるべき(許容するのが自然だと考えられる)理由です。
現実のTypeScriptではnever型に対するプロパティアクセスは許容されていないので、TypeScriptの型付けは「導出木が存在する」という原則から逸脱している、ということになります。あるいは、プロパティアクセスの規則に「t : never を結論とする導出木が存在しない」というようなアドホックな条件がついている、と解釈することもできるかもしれません。
「存在するか」の判定は難しい
ここからはTypeScriptのnever型の話から外れた、雑談のようなものになります。
型付けを「導出木が存在すること」によって定義したことで、型の付いた項を(規則の範囲で)自由に組み合わせて作った大きな項にも型が付くことが保証されます。これでめでたしめでたしでしょうか?
型検査器の実装のことを考えると、そうでもありません。実は、型システムが複雑になると「導出木が存在すること」の判定が難しくなります。
一般論として、「何かが存在すること」をアルゴリズムで判定するのは難しい問題です。数学の難問、フェルマーの最終定理もリーマン予想もコラッツ問題も、「何かが存在するかどうか」の問いです。プログラムを組んで計算機をぶん回すだけで数学の難問が解けたらどんなに良いでしょう。
型付けの判定、つまり「導出木が存在するか」はどうでしょうか。型システムが簡単なうちは問題ありません。型付けしたい項を見ればそれを結論とする規則は限られているので、判定のアルゴリズムを組めます。
型システムが複雑になってくると、「導出木が存在するか」のアルゴリズムを組むのが難しくなってきます。特に、部分型付けの包摂規則
が厄介で、t : T という目標があったときに t : T を結論とする規則を探索すればいいのか、t : S を結論とする規則を探索すればいいのかわかりません。部分型関係の推移律にも似たような問題があります。
複雑な型システムに対する型検査のアルゴリズムを組むには、型付けの「仕様」(自然な規則の集合によって型システムが与えられ、「導出木が存在するか」で項の型付けが定義される)と「実装」(実装しやすい規則の集合およびアルゴリズム)を分けて考える必要が出てきます。「型システム入門」で言うところの「アルゴリズム的型付け」が後者で、「第16章 部分型付けのメタ理論」で扱われています。アルゴリズム的型付けもやはり「導出木が存在するか」で定義されていますが、使用する規則の集合が異なり、特に包摂規則を組み込んでいません。
もしnever型とプロパティアクセスをもつ真っ当な型システムを実装する場合、never型に対するプロパティアクセスを許容するにはそれ用の規則をアルゴリズム的型付けに追加する必要があるでしょう。しかし、それは「never型に対するプロパティアクセスを許容しないのが自然だ」ということを意味するのではなく、「自然な仕様を実現するために必要なコスト」となります。「型システム入門」では、「16.4 アルゴリズム的型付けとBottom型」でこのことが取り上げられています。
他の話題
型付けの特徴付け(好きな規則を集めて、「導出木が存在すること」で定義する)と、型検査のアルゴリズムの兼ね合いを掘り下げると、双方向型付け (bidirectional typing) の話題に行き着くかもしれない……と思いましたが、疲れたのでやめておきます。
双方向型付けについては、前に書いた記事「「型システム入門」の先へ:TypeScriptの型システムのいくつかの側面」で簡単に取り上げました。
宣伝:「型システムのしくみ TypeScriptで実装しながら学ぶ型とプログラミング言語」
今年の4月に、遠藤侑介 著「型システムのしくみ」という本がラムダノートから出版されました。この本は、TypeScriptのサブセットのような言語の型検査器を作ることで型システムを学ぶ、というような本です。「型システム入門」は理論も充実した教科書ですが、「型システムのしくみ」は実践から入るので、「型システムのしくみ」の方がとっつきやすい人もいるかもしれません。
『型システムのしくみ ― TypeScriptで実装しながら学ぶ型とプログラミング言語』 – 技術書出版と販売のラムダノート
1冊頂いたので、移動中などに読み進めています。まだ4章までしか読めていませんが……。
この本は型システムの設計者の気持ちにも触れられていて(例:第2章のコラム「TypeScriptで『1+true』はなぜNGなのか?」)、型システムは絶対ではなく、設計の余地があることが強調されています。この記事と前回の記事で取り上げた「never型のプロパティアクセスを許容するか」という問題も、「こうするのが絶対」ということではなく、設計者の選択次第でした(この記事でも「never型のプロパティアクセスは許容するのが自然」とは書きましたが、「許容しなければならない」とまでは書いていません)。
読み終わったら改めてレビュー記事を書くかもしれませんが、良い機会なので宣伝でした。